Lista de exercícios sobre teorema de Tales

Confira uma lista de exercícios resolvidos que preparamos sobre o teorema de Tales!

Por Elainy Marciano Publicado em 12/06/2020 - 15:35

O teorema de Tales relaciona as medidas de retas paralelas cortadas por retas transversais.

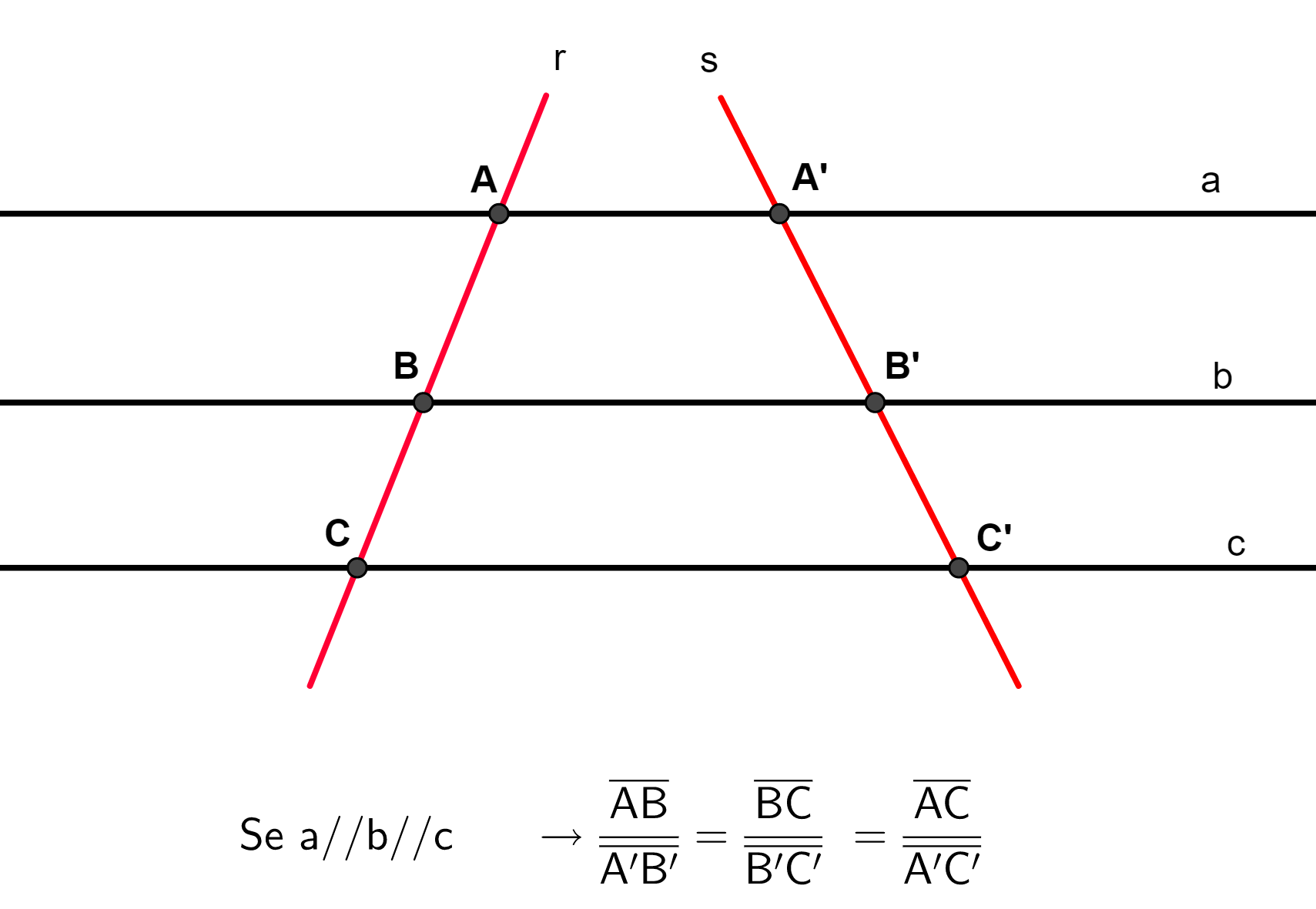
Considere duas retas r e s, não paralelas, que cruzam três retas paralelas a, b e c. Pelo teorema de Tales, os segmentos da reta r são proporcionais aos segmentos da reta s, isto é:

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

MEC suspende autorização de novos cursos à distância

Para aprender mais sobre esse assunto, confira uma lista de exercícios sobre teorema de Tales.

Lista de exercícios sobre teorema de Tales

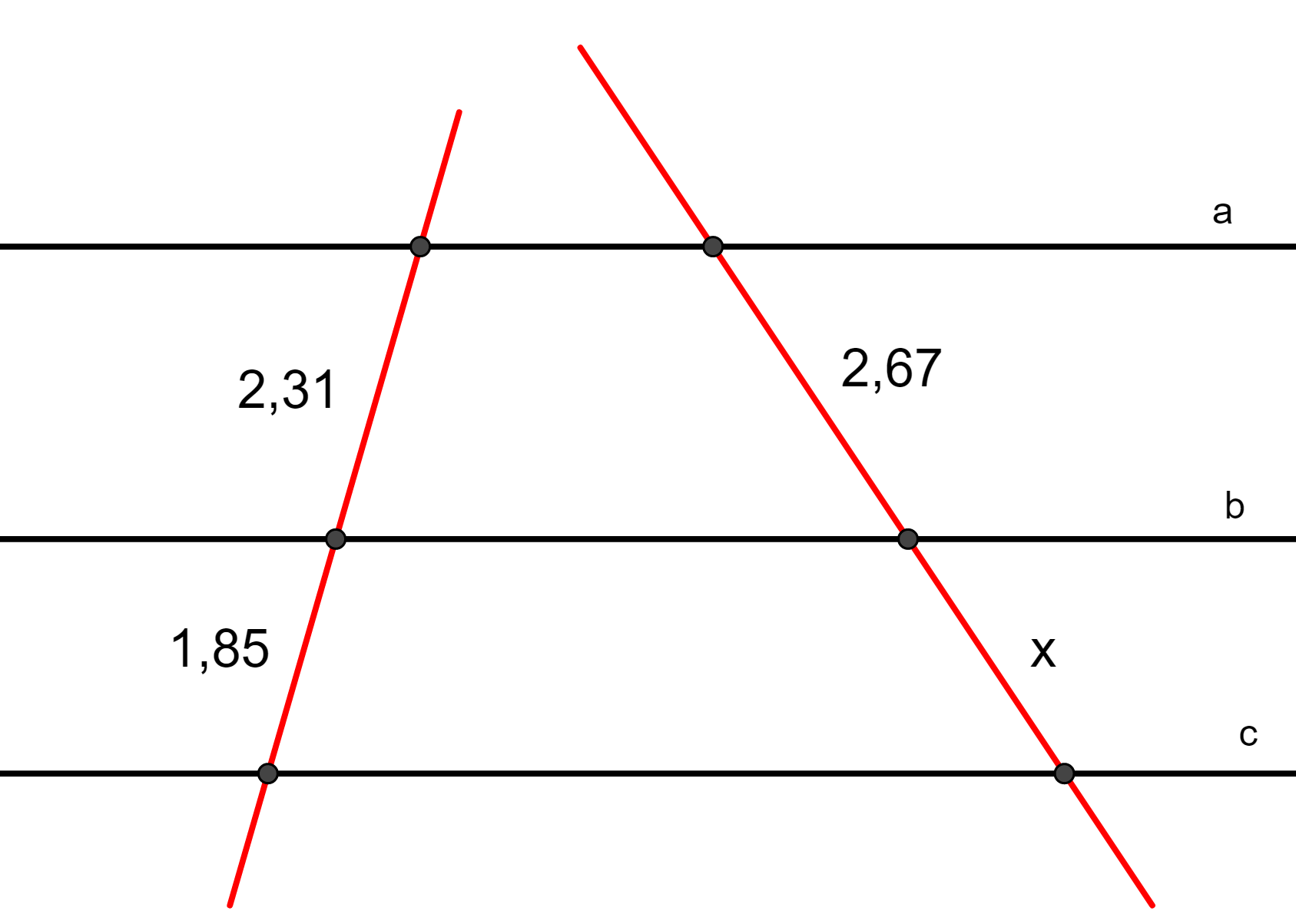
Questão 1. Determine o valor de x, sabendo que a//b//c.

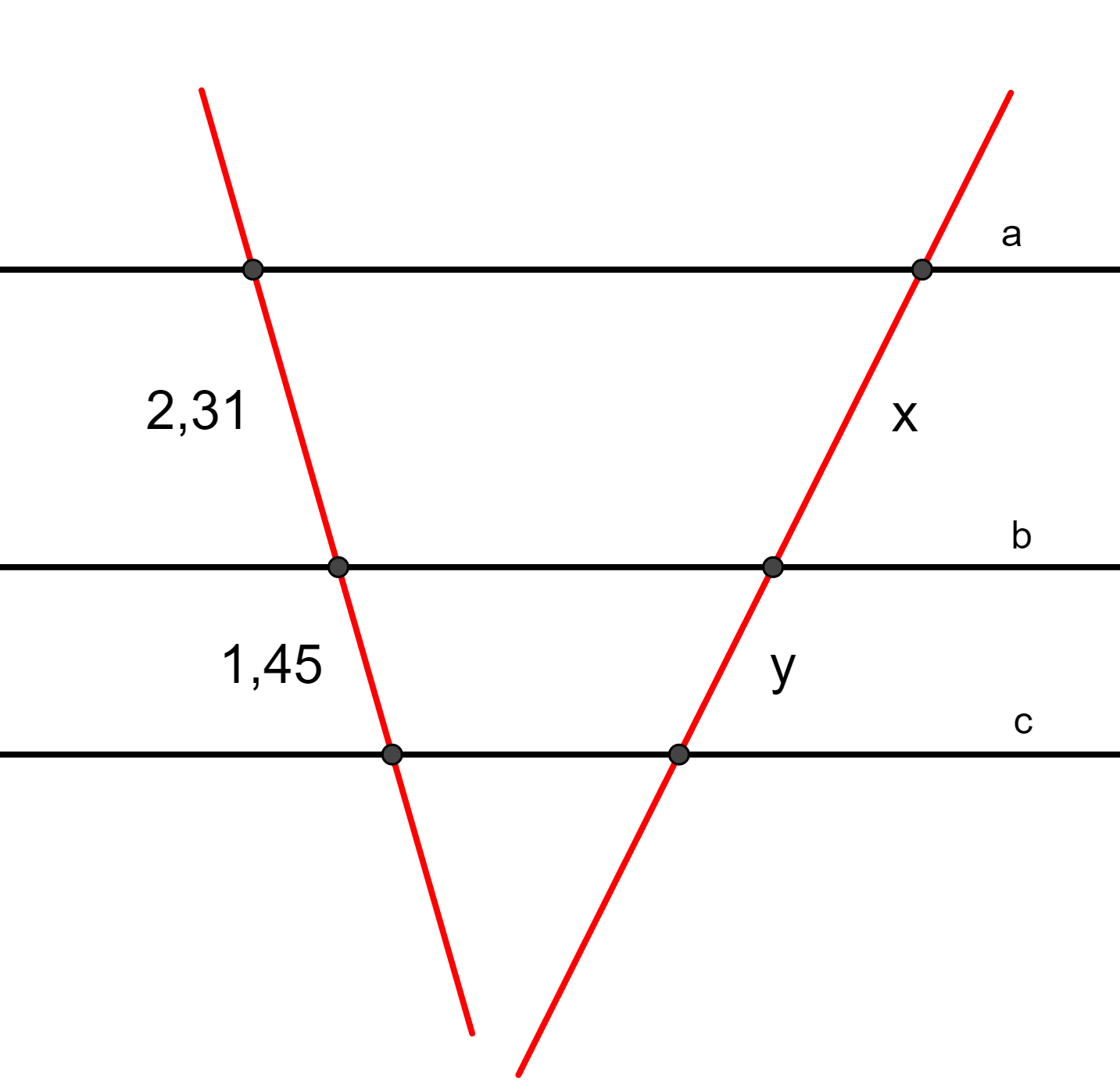
Questão 2. Determine os valores de x e y, considerando que x + y = 4,04 e a//b//c.

Questão 3. Encontre o valor de x, sabendo que a\\b\\c.

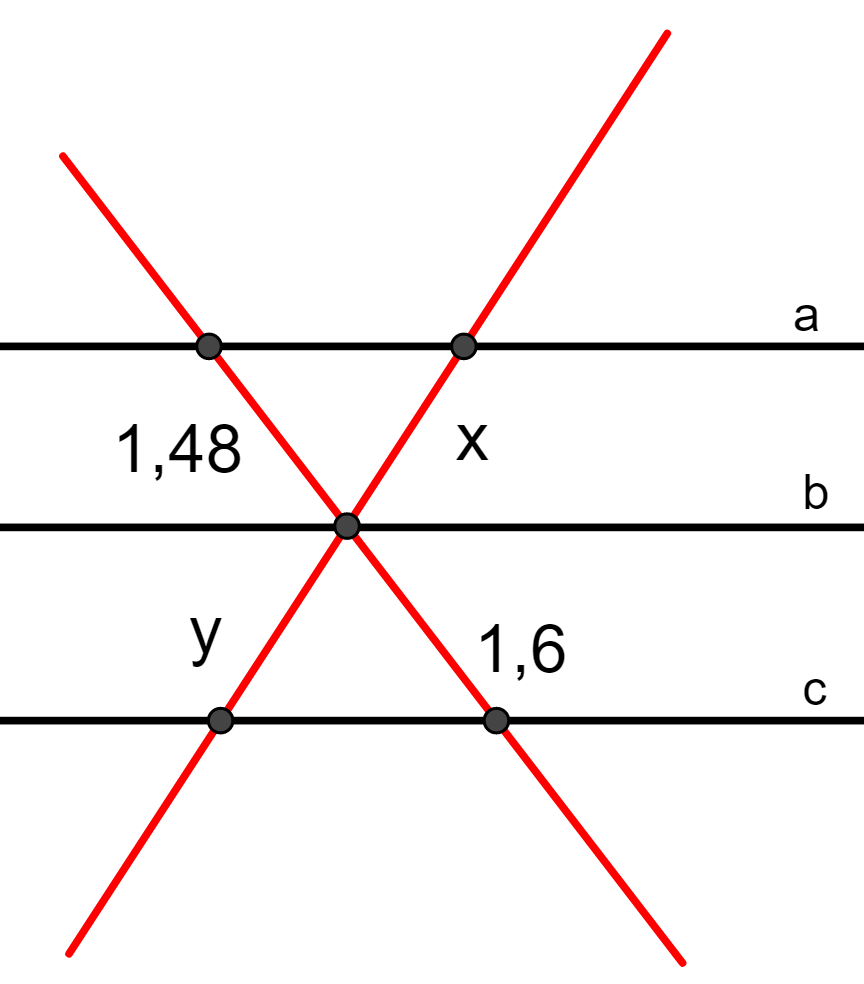
Questão 4. Determine os valores de x e y, considerando que y + x = 2,91 e a//b//c.

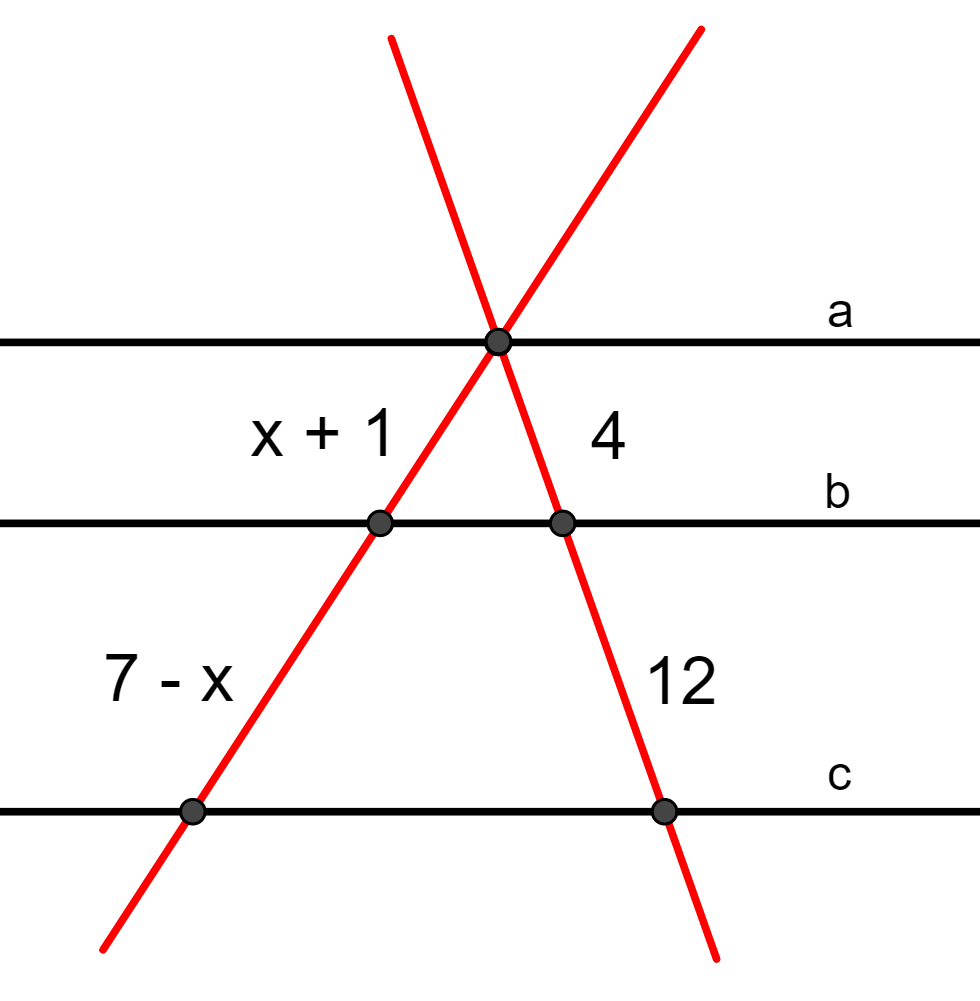
Questão 5. Sabendo que a//b//c, determine o valor de x.

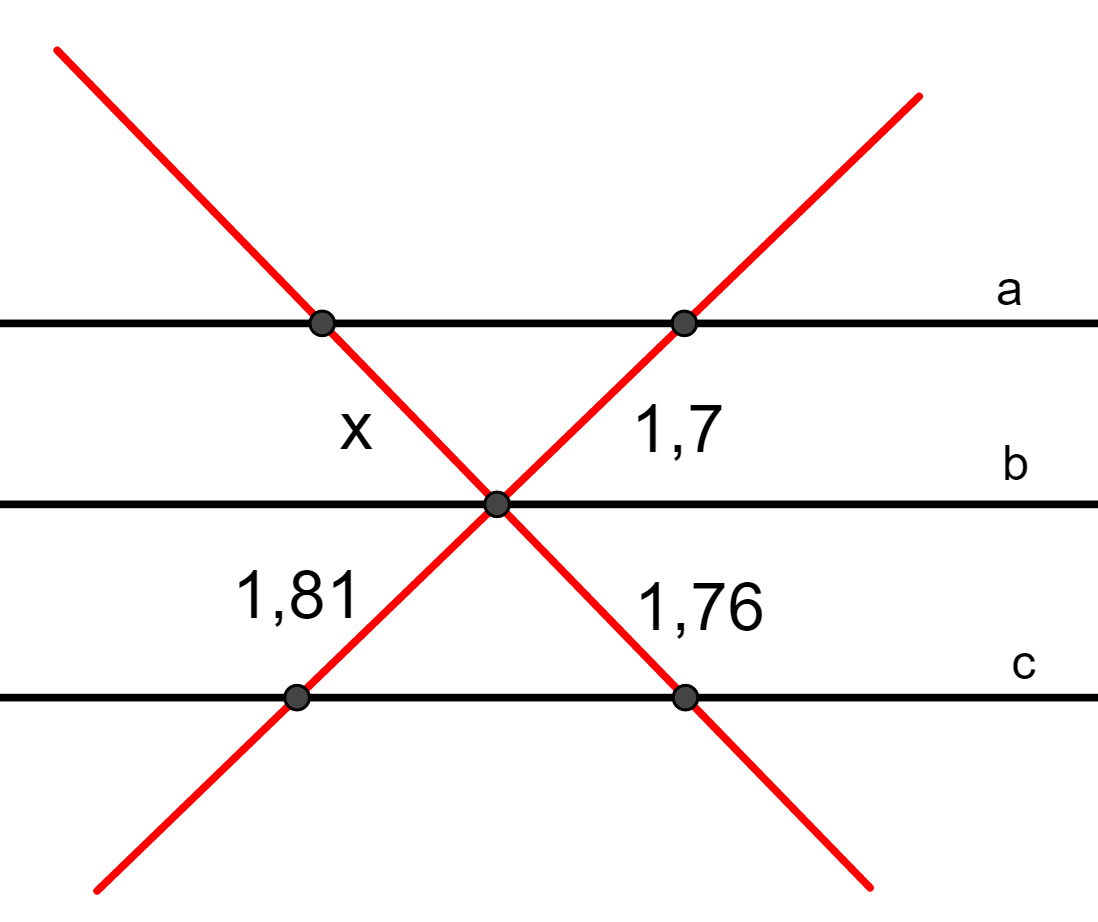
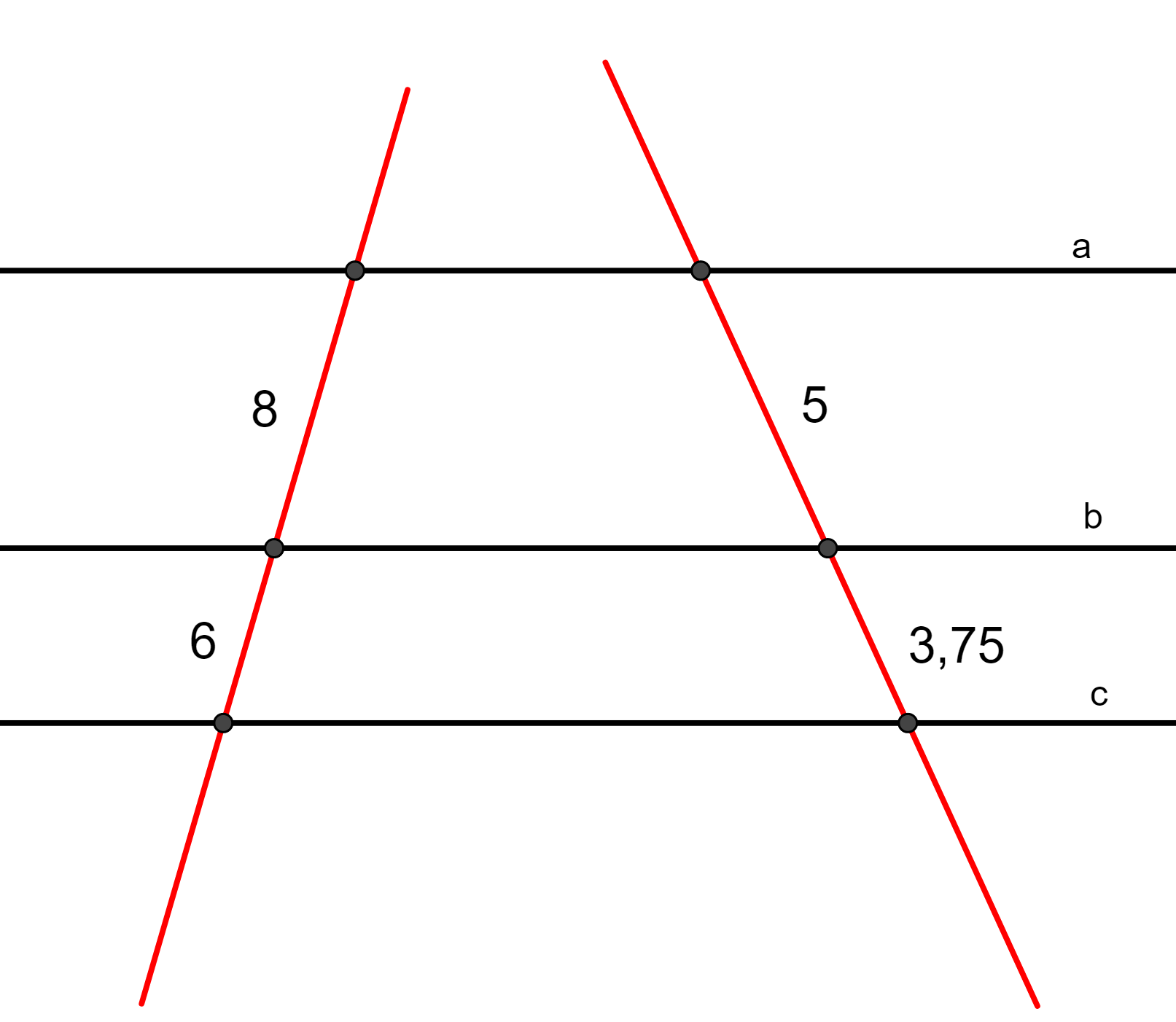
Questão 6. As retas a e b são paralelas. Verifique, pelo teorema de Tales, que a reta c também é paralela.

Resolução da questão 1

Pelo teorema de Tales, os segmentos são proporcionais, ou seja:

$\dpi{120} \frac{2,31}{2,67} = \frac{1,85}{\mathrm{x}}$

Multiplicando cruzado, obtemos o valor de x:

2,31x = 4,94 ⇒ x = 4,94/2,31 ⇒ x = 2,14

Resolução da questão 2

Pelo teorema de Tales, os segmentos são proporcionais, ou seja:

$\dpi{120} \frac{2,31}{\mathrm{x}} = \frac{1,45}{\mathrm{y}}$

Como x + y = 4,04 ⇒ y = 4,04 – x.

Substituindo y por 4,04 – x, temos:

$\dpi{120} \frac{2,31}{\mathrm{x}} = \frac{1,45}{4,04 - \mathrm{x}}$

Multiplicando cruzado, obtemos o valor de x:

1,45x = 2,31.(4,04 – x) ⇒ 1,45x = 9,33 – 2,31x ⇒ 1,45x + 2,31x = 9,33

⇒ 3,76x = 9,33 ⇒ x = 9,33/3,76 ⇒ x = 2,48

Substituindo o valor de x na expressão y = 4,04 – x, obtemos o valor de y:

y = 4,04 – x ⇒ y = 4,04 – 2,48 ⇒ y = 1,56

Resolução da questão 3

Pelo teorema de Tales, os segmentos são proporcionais, ou seja:

$\dpi{120} \frac{\mathrm{x}}{1,7} = \frac{1,76}{1,81}$

Multiplicando cruzado, obtemos o valor de x:

1,81x = 2,98 ⇒ x = 2,98/1,81 ⇒ x = 1,65

Resolução da questão 4

Pelo teorema de Tales, os segmentos são proporcionais, ou seja:

$\dpi{120} \frac{1,5}{\mathrm{x}} = \frac{1,58}{\mathrm{y}}$

Como y + x = 2,91 ⇒ y = 2,91 – x.

Substituindo o valor de y por 2,91 – x, temos que:

$\dpi{120} \frac{1,48}{\mathrm{x}} = \frac{1,6}{2,91 - \mathrm{x}}$

Multiplicando cruzado, obtemos o valor de x:

1,6x = 1,48.(2,91 – x) ⇒ 1,6x = 4,31 – 1,48x ⇒ 1,6x + 1,48x = 4,31

⇒ 3,08x = 4,31 ⇒ x = 4,31/3,08 ⇒ x = 1,4

Substituindo o valor de x na expressão y = 2,91 – x, obtemos o valor de y:

y = 2,91 – x ⇒ y = 2,91 – 1,4 ⇒ y = 1,51

Resolução da questão 5

Pelo teorema de Tales, os segmentos são proporcionais, ou seja:

$\dpi{120} \frac{\mathrm{x} + 1}{4} = \frac{7 - \mathrm{x}}{12}$

Multiplicando cruzado, obtemos o valor de x:

12.(x + 1) = 4.(7 – x) ⇒ 12x + 12 = 28 – 4x ⇒ 12x + 4x = 28 – 12

⇒ 16x = 16 ⇒ x = 16/16 ⇒ x = 1

Resolução da questão 6

Para mostrar que a reta c também é paralela, basta mostrar que os segmentos das retas transversais são proporcionais.

A razão do primeiro segmento é:

$\dpi{120} \frac{8}{5} = 1,6$

E a razão do segundo segmento é:

$\dpi{120} \frac{6}{3,75} = 1,6$

Como a razão é a mesma, os segmentos são proporcionais. Portanto, satisfaz o teorema de Tales e a reta c é paralela também.

Você também pode se interessar:

Exercícios de matemática resolvidos Exercícios resolvidos sobre teorema de Tales