Utilizando as relações trigonométricas
Saiba quais são e como utilizar as relações trigonométricas: seno, cosseno e tangente, em um triângulo retângulo.
As relações trigonométricas são fórmulas que relacionam os ângulos e os lados de um triângulo retângulo. Essas fórmulas envolvem as funções seno, cosseno e tangente e possuem muitas aplicações em problemas geométricos envolvendo esse tipo de triângulo.
Relações trigonométricas no triângulo retângulo
O triângulo retângulo é o triângulo que possui um ângulo reto (90°) e dois ângulos agudos (menores que 90°). Os lados do triângulo retângulo são chamados de hipotenusa e catetos, sendo que os catetos podem ser oposto ou adjacente, conforme o ângulo de referência.
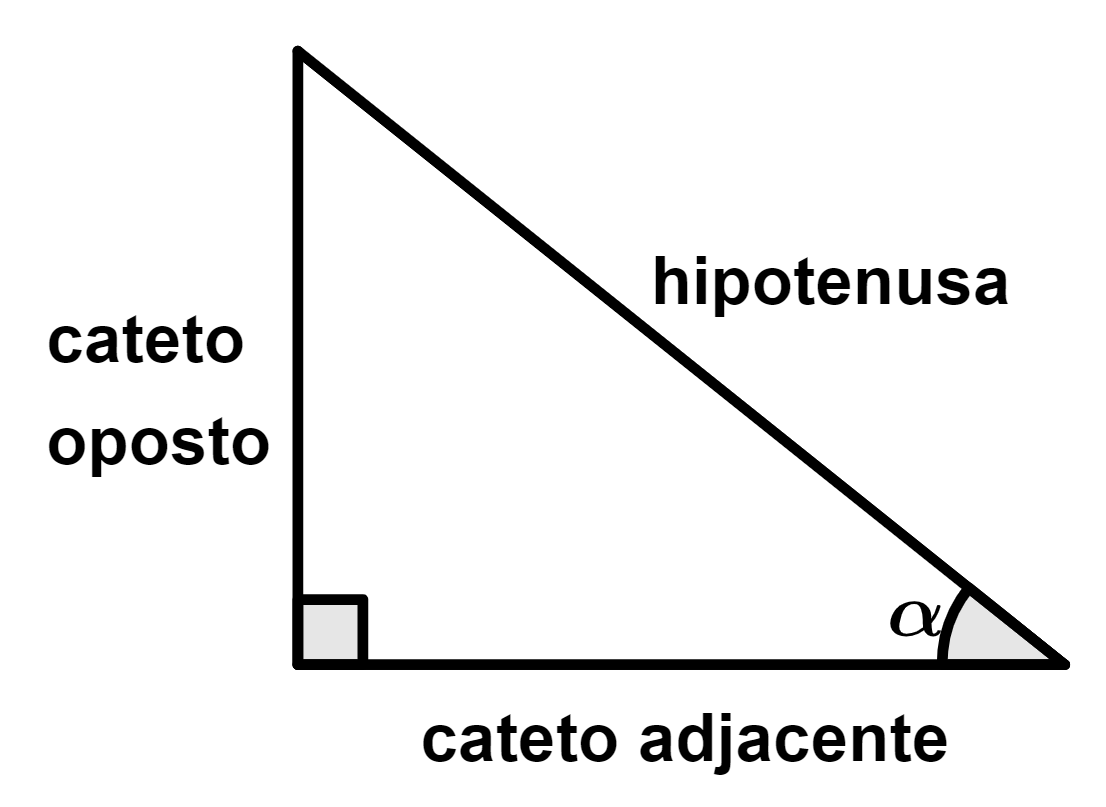
Elementos do triângulo retângulo:
- Hipotenusa: lado oposto ao ângulo reto;
- Cateto oposto: lado oposto ao ângulo agudo considerado;
- Cateto adjacente: lado consecutivo ao ângulo agudo considerado.
Fórmulas:
Considerando o ângulo do triângulo retângulo, temos que:
Exemplos – Utilizando as relações trigonométricas
Veja, a seguir, exemplos de como utilizar as relações trigonométricas.
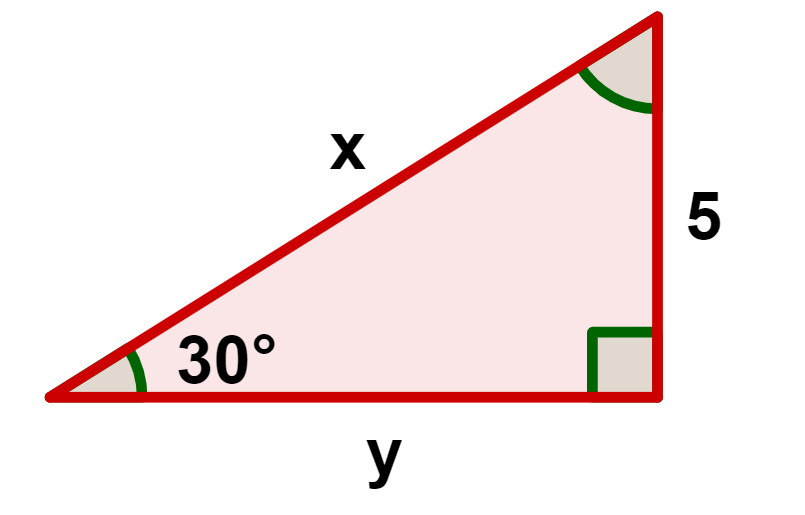
Exemplo 1: Calcule o valor de x e y no triângulo abaixo:
Pelo seno do ângulo de 30°, podemos determinar o valor de x, que é a hipotenusa do triângulo.
Agora, uma das formas de encontrar o valor de y, é a partir do cosseno do ângulo de 30°. Nesse caso, y é o cateto adjacente ao ângulo de 30°.
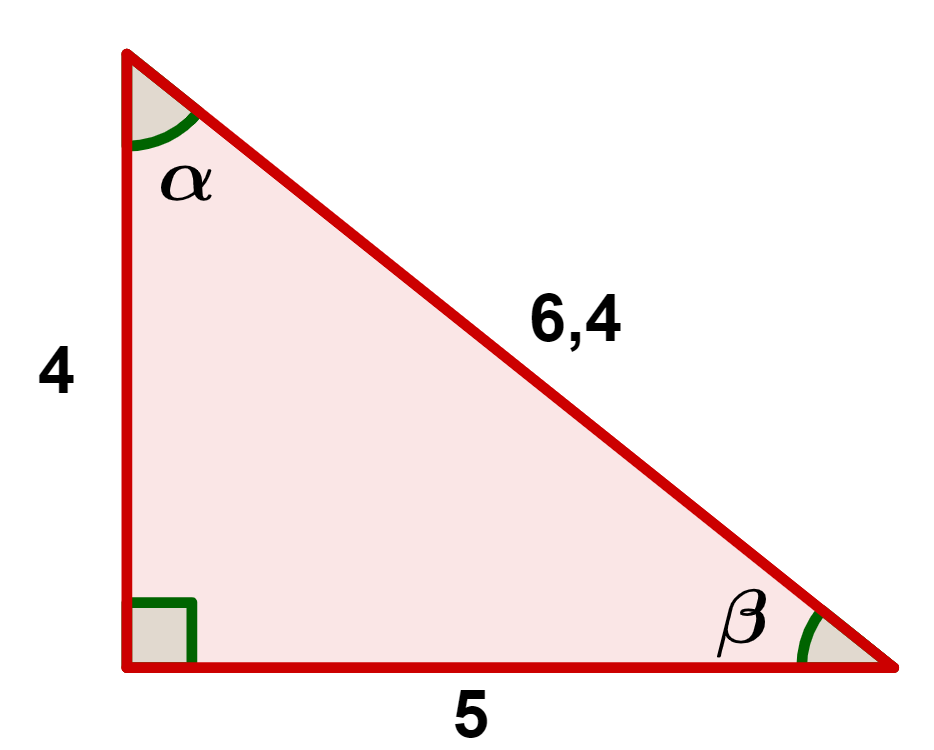
Exemplo 2: Determine a medida dos ângulos e
do triângulo abaixo:
Primeiro, vamos determinar o ângulo :
Agora, vamos determinar o ângulo :
Observe que utilizamos o seno nos dois casos, mas também poderíamos utilizar o cosseno e chegar nesses mesmos resultados.
Você também pode se interessar:
- Tabela trigonométrica
- Círculo trigonométrico
- Relações derivadas
- Lista de exercícios de trigonometria
- Seno e cosseno de ângulos obtusos

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.