Relações trigonométricas
Aprenda sobre as relações ou identidades trigonométricas. Saiba quais são as relações fundamentais, as relações derivadas e outras relações úteis!
As relações trigonométricas ou identidades trigonométricas são relações entre as funções trigonométricas, que são verdadeiras para todos os valores do domínio das funções envolvidas.
As relações trigonométricas caracterizam-se como importantes ferramentas no cálculo de funções trigonométricas e na simplificação de expressões envolvendo essas funções.
Relações trigonométricas fundamentais
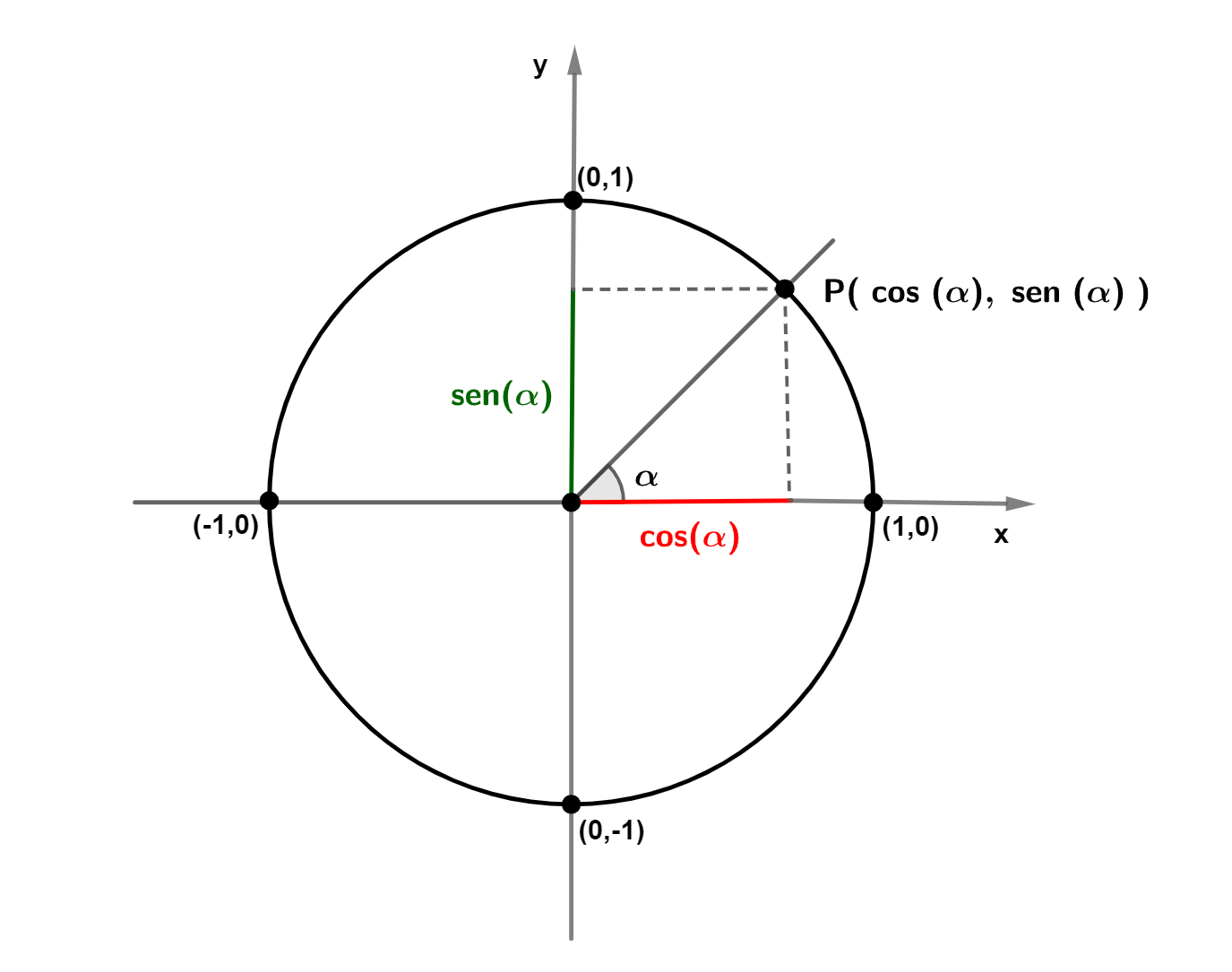
Para auxiliar no estudo das funções trigonométricas, utiliza-se o círculo trigonométrico, que é um círculo de raio 1 associado a um sistema de coordenadas no plano cartesiano.
O eixo x é o eixo dos cossenos e o eixo y, o eixo dos senos. Considerando um ângulo , teremos sempre um ponto P da circunferência associado a ele.
Observe, na figura, que há um triângulo retângulo com hipotenusa igual ao segmento que liga o centro ao ponto P e que tem valor igual a 1 (raio) e catetos iguais ao seno de e cosseno de
.
Assim, podemos utilizar o teorema de Pitágoras, que diz que a hipotenusa () ao quadrado é igual à soma dos quadrados dos catetos (
).
Dessa forma, obtemos a primeira relação fundamental, também conhecida por relação pitagórica:
Há, ainda, outras relações. Você se lembra que, no triângulo retângulo, uma das relações era que a tangente de um ângulo era calculada como o cateto oposto dividido pelo cateto adjacente?
Observe que no triângulo do círculo trigonométrico, o cateto oposto é o seno de e o cateto adjacente, o cosseno. Assim:
Além do seno, cosseno e tangente, outras funções trigonométricas importantes aparecem nas relações trigonométricas: secante (sec), cossecante (csc) e cotangente (cot).
Veja todas essas funções no círculo trigonométrico:
A secante é definida como o inverso da função cosseno:
Já a cossecante corresponde ao inverso da função seno:
Por fim, a cotangente é dada pelo inverso da função tangente:
Relações trigonométricas derivadas
As relações trigonométricas derivadas são relações obtidas a partir das relações fundamentais.
Dividindo todos os termos da equação por
e considerando outras relações que vimos, obtemos:
Semelhantemente, dividindo todos os termos da equação por
, podemos obter mais uma relação:
Outras relações
Além das relações fundamentais e derivadas, existem relações entre os valores das funções de ângulos complementares (somam 90°):
E de ângulos suplementares (somam 180°):
Você também pode se interessar:
- Razões trigonométricas
- Relações métricas no triângulo retângulo
- Tabela trigonométrica
- Ângulos notáveis
- Teorema de Tales

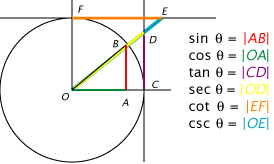
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.