Matrizes
Saiba o que são matrizes, quais os diferentes tipos, como obter a transposta e como fazer operações de soma, subtração e multiplicação entre matrizes.
O que é uma matriz? Uma matriz é, simplesmente, a representação de uma tabela de informações organizada em linhas e colunas. Normalmente, o número de linhas de uma matriz é indicado pela letra m, e o número de colunas, pela letra n.
Por que usar uma matriz? Organizar um conjunto de dados em uma matriz facilita na visualização e identificação de elementos, inclusão ou exclusão de valores, e realização de cálculos em uma mesma matriz ou entre diferentes matrizes.
Exemplo de matriz:
A tabela a seguir, apresenta as notas de alguns alunos em matemática. É uma tabela com 3 linhas e 2 colunas. Vamos representar essas informações em uma matriz.
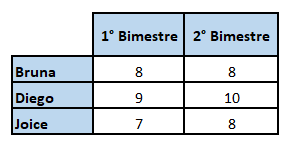
Assim, é uma matriz com 3 linhas e 2 colunas.
E podemos escrever → Lê-se matriz A de ordem 3 por 2.
Elementos de uma matriz
Uma matriz qualquer, com m linhas e n colunas, pode ser escrita da seguinte forma:
Em que:
O primeiro número do subíndice de cada elemento representa a linha onde o elemento está, e o segundo número, representa a coluna. Veja que:
- O elemento
está na linha 1 e coluna 1;
- O elemento
está na linha 1 e coluna 2;
- O elemento
está na linha 1 e coluna n;
- O elemento
está na linha 2 e coluna 1;
- O elemento
está na linha 2 e coluna 2;
E assim por diante.
De modo geral, os elementos de uma matriz são do tipo , onde i é um número entre 1 e m e j é um número entre 1 e n.
Tipos de matrizes
Existem alguns tipos específicos de matriz, vamos ver os principais.
Matriz linha: matriz com uma linha apenas (1 x n).
Matriz coluna: matriz com uma coluna apenas (m x 1).
Matriz nula: todos os elementos são iguais a zero.
Matriz quadrada: o número de linhas é igual ao número de colunas (n x n).
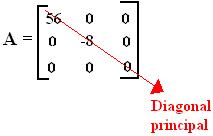
Matriz diagonal: é uma matriz quadrada em que todos os elementos que não fazem parte da diagonal principal são iguais a zero.
Matriz identidade: É uma matriz quadrada onde todos os elementos da diagonal principal são iguais a 1 e os outros elementos são iguais a zero. Em geral, esse tipo de matriz é representada pela letra I.
Leia mais: Tipos de matrizes
Matriz transposta
Considerando uma matriz A qualquer, a sua matriz transposta é uma outra matriz obtida quando escrevemos cada linha de A em forma de coluna.
Assim, a primeira linha corresponde à primeira coluna, a segunda linha linha corresponde à segunda coluna, e assim por diante.
Exemplo:
Operações com matrizes
- Adição e subtração de matrizes
Só podemos somar ou subtrair duas matrizes A e B se elas forem da mesma ordem, ou seja, o número de linhas de A é igual ao número de linhas de B e o número de colunas de A é igual ao número de colunas de B.
A soma ou subtração de A e B é feita entre os elementos de mesma posição.
Exemplo:
a) Soma de matrizes: A(2 x 2) + B(2 x 2) = C(2 x 2)
b) Subtração de matrizes: A(3 x 2) – B(3 x 2) = C(3 x 2)
Leia mais: Adição e subtração de matrizes
- Multiplicação de matrizes por um número real
Para fazer a multiplicação de uma matriz A por um número real, multiplicamos cada elemento da matriz A por esse número. O resultado é uma matriz de mesma ordem que a matriz A.
Exemplo: Multiplicar uma matriz A por 3.
- Multiplicação de matrizes
Para fazer a multiplicação de uma matriz A por uma matriz B, o número de colunas de A deve ser igual ao número de linhas de B.
A (m x p) e B (p x n) → A tem p colunas e B tem p linhas → Podemos multiplicar
O resultado da multiplicação será uma matriz de ordem m x n.
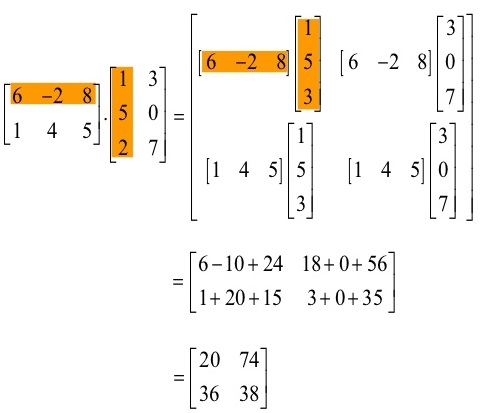
Exemplo: A(2 x 3) . B (3 x 2) = C( 2 x 2)
Você também pode se interessar:
- Lista de exercícios de matrizes
- Escalonamento de matrizes – Resolver sistemas lineares
- Regra de sinais
- Sistemas de equações
- Expressões algébricas
- Regra de três – Veja os tipos e aprenda como calcular

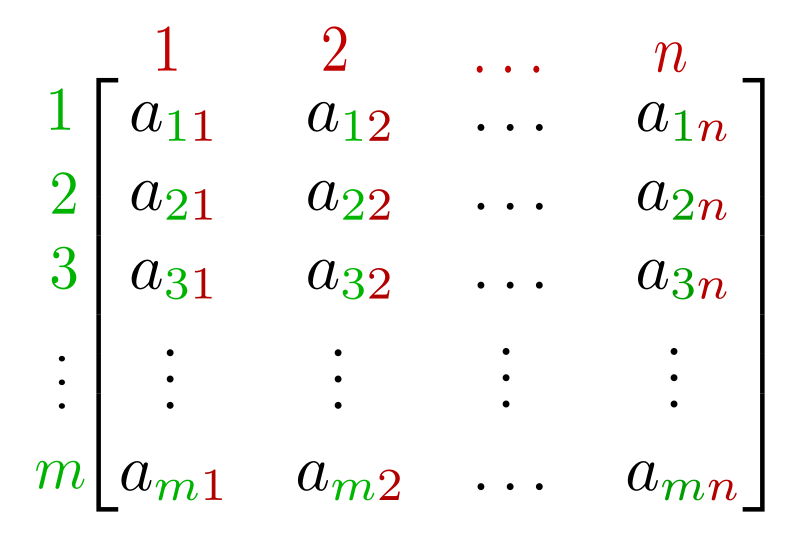
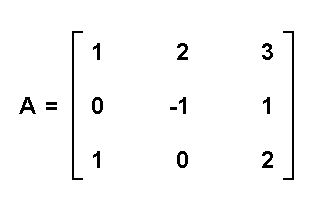
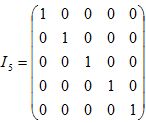
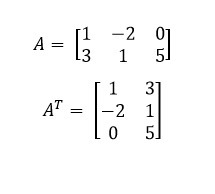
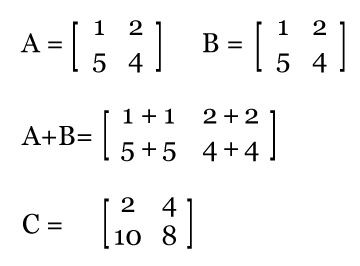
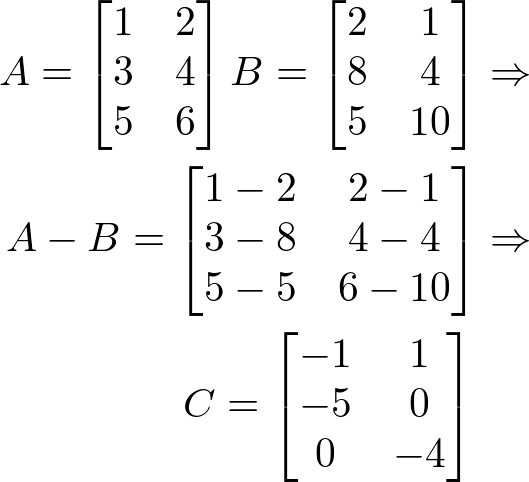

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.