Retângulo
O retângulo é uma figura geométrica plana. Aprenda a calcular a área, o perímetro, a medida da diagonal e a soma dos ângulos internos e externos.
O retângulo é uma figura geométrica plana, que se classifica como um quadrilátero, por possuir quatro lados.
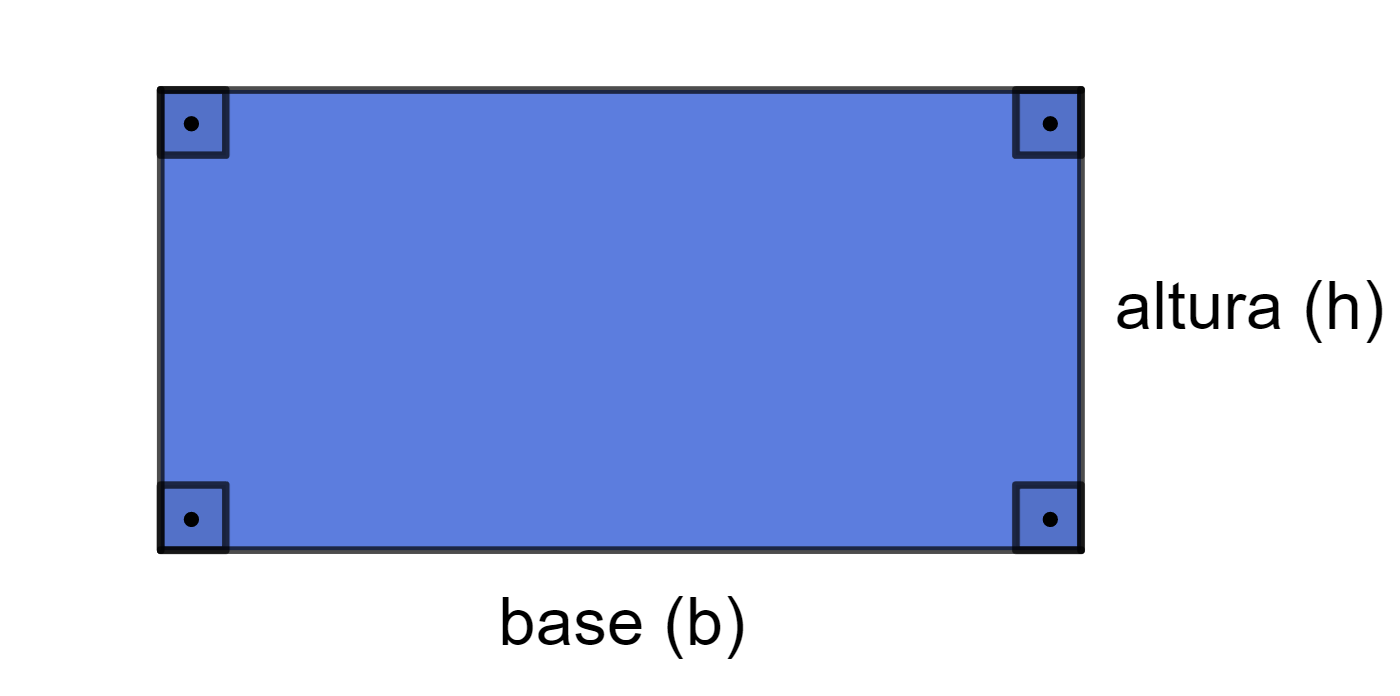
Ele é formado por dois lados maiores, de mesmo tamanho e paralelos, e dois lados menores, também de mesmo tamanho e paralelos. Portanto, retângulos são um tipo específico de paralelogramo.
O lado maior é chamado de base do retângulo, e o lado menor é a altura do retângulo.
Outra característica fundamental dos retângulos é que todos os quatro ângulos internos são ângulos retos (medem 90°).
Área do retângulo
A área do retângulo é dada pelo produto entre a medida da base e a altura. Assim, a fórmula da área do retângulo é:
Em que:
: medida da base do retângulo;
: altura do retângulo.
Exemplo: Calcular a área de um retângulo cuja base mede 20 cm e a altura é metade da medida da base.
Temos b = 20 e h = 20/2 = 10, já que a altura é metade da base.
Aplicando esses valores na fórmula da área, temos:
A = 20 . 10 = 200
Portanto, a área do retângulo é igual a 200 cm².
Devemos ficar atentos à unidade de medida da área, que deve ser sempre elevada ao quadrado (cm², m², etc.)
Perímetro do retângulo
O perímetro do retângulo é dada pela soma das medidas dos seus quatro lados, isto é:
Assim, temos a fórmula do perímetro do retângulo:
Exemplo: Calcular o perímetro de um retângulo cuja base mede 8 cm e altura mede 6 cm.
P = 2 . (8 + 6)
P = 2 . 14
P = 28
Então, o perímetro do retângulo é igual a 28 cm.
Atenção! Diferente da área, a unidade de medida do perímetro é a mesma da base e da altura do retângulo.
Diagonal do retângulo
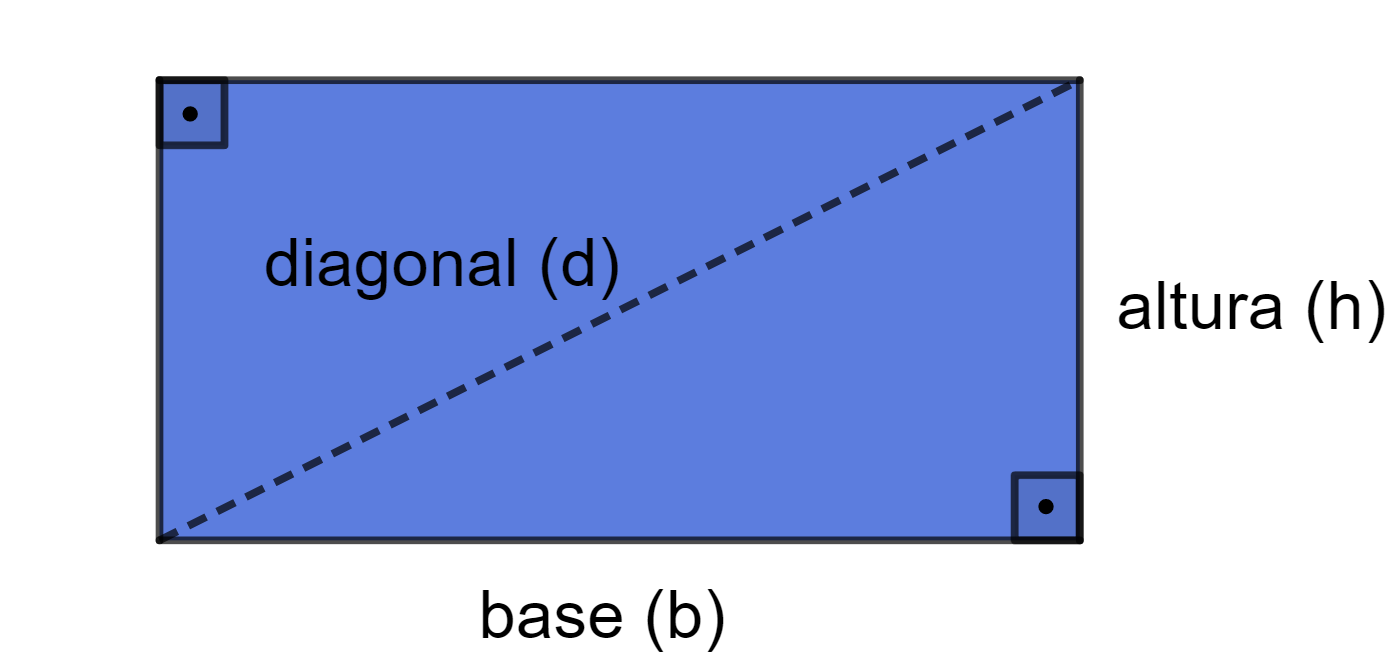
O retângulo possui duas diagonais. As diagonais são os segmentos de reta que ligam dois vértices não consecutivos, ou seja, são segmentos de reta que devem passar pelo meio da figura.
A fórmula da diagonal do retângulo é:
Para mostrar que isso é verdade, basta observarmos que a diagonal divide o retângulo em dois triângulos retângulos.
Dessa forma, podemos utilizar o Teorema de Pitágoras para determinar a diagonal (d), que é a hipotenusa do triângulo retângulo de catetos b e h.
Temos que:
Aplicando a raiz quadrada em ambos os lados da equação, temos a fórmula que apresentamos antes.
Exemplo: Encontrar a medida da diagonal de um retângulo cuja base mede 12 cm e a altura é igual a 9 cm.
Ou seja, a diagonal do retângulo mede 15 cm.
Ângulos do retângulo
Os ângulos internos do retângulo são todos iguais a 90°. Assim, a soma dos seus ângulos internos é sempre igual a 360°.
Além disso, os ângulos internos e externos do retângulo são suplementares, ou seja, juntos formam um ângulo de 180°, então, os ângulos externos do retângulo também medem todos 90°.
A soma dos ângulos externos do retângulo é igual a 360°.
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.