Área do cilindro

Objetos com forma de cilindro são comuns no dia a dia, são aqueles que possuem um corpo redondo, alongado e com três dimensões: largura, altura e profundidade. Assim, é bastante comum o interesse em calcular a área do cilindro.

A área é uma medida calculada para figuras de apenas duas dimensões, as figuras planas, pois corresponde à medida de uma superfície. Então, quando falamos em calcular a área de um cilindro, falamos em calcular a sua área externa, por isso, devemos pensar na planificação do cilindro.

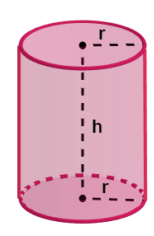
Considere um cilindro como o da figura abaixo:

Onde:

• h: altura do cilindro
• r: raio da base

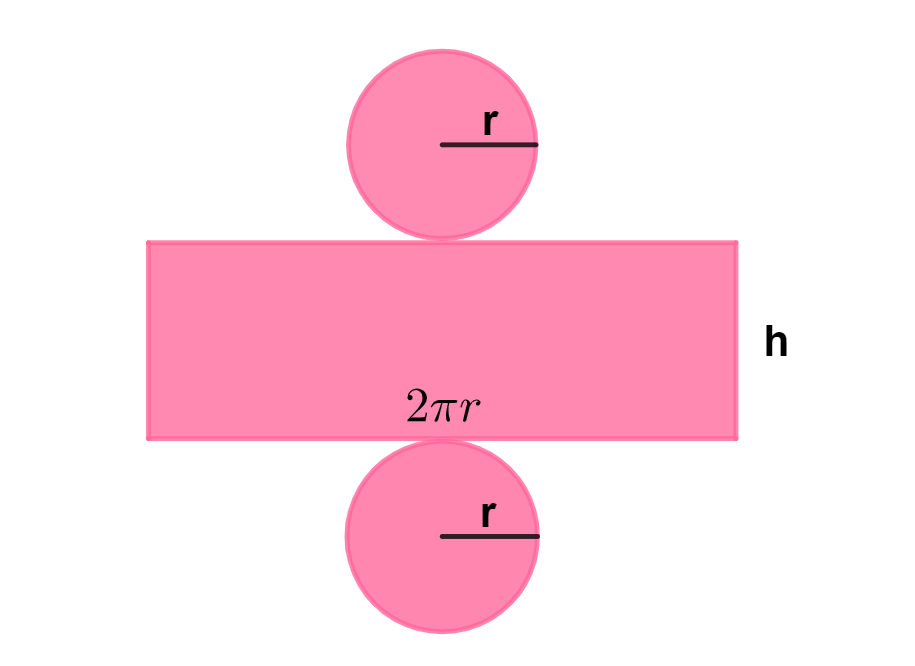
A planificação do cilindro corresponde a três figuras geométricas planas: dois círculos e um paralelogramo.

Desse modo, para calcular a área externa de um cilindro, tudo o que temos que fazer é calcular, separadamente, a área de cada uma dessas três figuras e depois somar.

Área lateral

A área lateral é a área de um paralelogramo, que é obtida quando multiplicamos a largura pela altura da figura:

Onde:

• h: altura do cilindro
• r: raio da base
• 

Área da base

A base de um cilindro é um círculo de raio r. Assim, a área da base é dada por:

Onde:

• r: raio da base
• 

Área total

A área total é a área externa do cilindro e corresponde a soma da área lateral mais a área de cada uma das bases.

Onde:

• h: altura do cilindro
• r: raio da base
• 

Exemplo: A base de um cilindro tem raio medindo 3 cm e altura igual a 9 cm. Calcule:

a) A área lateral

Temos r = 3 e h = 9. Substituindo na fórmula da área lateral, temos que:

Logo, a área lateral do cilindro mede 169,56 cm².

b) A área da base

Assim, a área de cada base é igual a 28,26 cm².

c) A área total

Portanto, a área total é igual a 226,08 cm².

Você também pode se interessar:

• Cone
• Paralelepípedo
• Cubo