Como fazer conta de dividir

A divisão é uma operação matemática básica, cuja ideia principal é dividir uma quantidade em partes iguais.

No entanto, existem algumas situações onde a divisão não é tão trivial e apresenta algumas “pegadinhas”, as quais as pessoas costumam errar.

Pensando nisso, preparamos um texto sobre como fazer conta de dividir.

Vamos te mostrar os elementos da divisão, o que fazer com o resto, como fazer prova real, como dividir por números com dois algarismos, como dividir um número menor por um número maior e quando acrescentar zeros no quociente.

Elementos da divisão

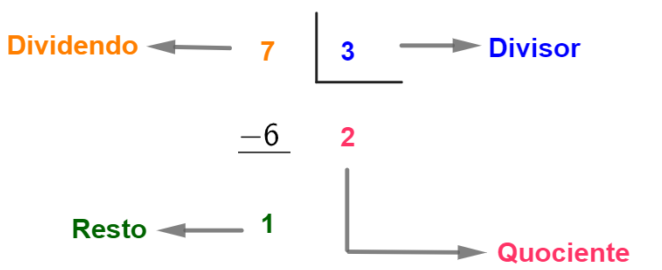
Os elementos da divisão são: dividendo, divisor, quociente e resto.

• Dividendo: número que queremos dividir;
• Divisor: número pelo qual iremos dividir o dividendo;
• Quociente: resultado da divisão;
• Resto: número menor que o quociente, que sobra na divisão.

Exemplo: Dividir 7 por 3.

Nessa conta, o dividendo é o número 7, o divisor é o número 3, o quociente é 2 e o resto é 1.

Isso significa que se dividirmos 7 unidades em 3 partes iguais, cada parte será igual a 2 unidades e ainda sobra 1 unidade.

Para saber mais, leia nosso texto sobre algoritmo da divisão.

Resto da divisão

O resto da divisão é um valor que pode sobrar quando efetuamos uma conta de dividir. Em relação ao resto, podemos ter dois tipos de divisões.

• Divisão exata: quando não sobra nada, ou seja, o resto igual a zero.
• Divisão não exata: quando sobra alguma quantidade, ou seja, o resto é diferente de zero.

Mas o que fazer com o resto em divisões não exatas?

Se o quociente (resultado da divisão) tiver que ser um número inteiro, então, paramos a conta ali mesmo no resto. O resto poderá ter alguns significados diferentes de acordo com o problema.

Para entender mais sobre isso, leia nosso texto Para que serve o resto da divisão?

No entanto, quando o resultado puder ser um número não inteiro, então, ainda podemos dividir o resto pelo divisor. Na conta do exemplo, seria dividir 1 por 3, onde o resultado seria um número decimal.

Prova real na divisão

A prova real nas operações matemáticas é uma forma de comprovar se um resultado obtido está ou não correto.

Na divisão com resto igual a zero, a prova real consiste em multiplicar o quociente pelo divisor. Se o resultado dessa multiplicação for igual ao dividendo, então, a conta de divisão está correta.

dividendo = divisor × quociente

Já na divisão com resto diferente de zero, ainda devemos somar o resto a essa multiplicação, ou seja:

dividendo = divisor × quociente + resto

Divisão com dois algarismos no divisor

A divisão com dois algarismos no divisor é semelhante à divisão com um algarismo no divisor. O que fazemos é considerar os algarismos do dividendo que formem um número maior que o divisor.

Veja como fazer isso a partir de um exemplo.

Exemplo: 192 ÷ 16 = ?

19′ 2 | 16
-16   1
03

Observe que não dividimos 192 diretamente por 16. Consideramos os dois primeiros algarismos 1 e 9, pois 19 é maior que 16.

Depois, descemos o 2 e continuamos com a divisão.

19′ 2 | 16
-16↓   12
032
-32
00

Prova real: 16 × 12 = 192.

Divisão com dividendo menor que o divisor

A divisão com dividendo menor que o divisor é uma divisão de um número menor por um número maior.

Para resolver esse tipo de conta, acrescentamos um zero no dividendo e um zero e uma vírgula no quociente.

Se ainda não for possível fazer a divisão, acrescentamos mais um zero no dividendo e um zero no quociente, e assim por diante, até que o dividendo seja maior que o divisor.

O resultado desse tipo de divisão sempre será um número decimal, ou seja, um número com vírgula.

Exemplo: 3 ÷ 60 = ?

3 0 | 60
00000,

Observe que 30 ainda é menor que 60. Então, acrescentamos um zero no dividendo e um zero no quociente. Não acrescentamos outra vírgula, a vírgula é acrescentada uma única vez!

3 00 | 60
-300  0,05
000

Prova real: 60 × 0,05 = 3.

Divisão com zero no quociente

Em algumas situações, é necessário acrescentar zeros no quociente de uma divisão, como quando descemos um número, mas ele é menor que o divisor.

Para entender como isso funciona, vamos ver alguns exemplos.

Exemplo: 1560 ÷ 15 = ?

15′ 60   |15
-15 ↓↓   104
00 60
— -60
 —-00

Observe que descemos o 6, mas ele é menor que 15, não podemos dividir. Então, acrescentamos o zero no quociente.

Em seguida, descemos o 0. Agora, 60 é maior que 15, podemos dividir.

Chegamos numa divisão com resto igual a zero, ou seja, uma divisão exata.

Prova real: 104 × 15 = 1560.

Exemplo: 302 ÷ 5 = ?

30′ 2   | 5
-30↓    60
00 2

Observe que descemos o 2, mas ele é menor que 5, não podemos dividir. Então, acrescentamos o zero no quociente.

Contudo, veja que não temos mais nenhum número para descer. Então, trata-se de uma divisão não exata com resto igual a 2.

Prova real = 60 × 5 + 2 = 300 + 2  = 302.

Mas, se o quociente não precisar ser um número inteiro, podemos continuar dividindo e obter, como quociente, um número decimal.

30′ 2   | 5
-30↓    60,4
00 20
 0-20
0  00

Veja que acrescentamos um zero ao número que queremos dividir, o 2 nesse caso, e acrescentamos uma vírgula no quociente.

Prova real: 60,4 × 5 = 302

Você também pode se interessar:

• Divisão por zero
• Divisão de números decimais – Veja como dividir números com vírgula
• Lista de exercícios sobre divisão de números naturais
• Multiplicação e divisão de números negativos
• Critérios de divisibilidade