Concavidade da parábola
Entenda o que é concavidade da parábola, tipos de concavidade, o vértice e o ponto de máximo ou de mínimo em uma parábola.
Uma parábola é a representação gráfica no plano cartesiano de qualquer função quadrática. As funções quadráticas possuem a seguinte forma:
Sendo a, b e c números reais e a um número diferente de zero.
Concavidade da parábola
Uma parábola é sempre uma curva, que possui uma abertura. Essa abertura pode estar voltada para cima ou voltada para baixo.
Quando a abertura está voltada para cima dizemos que a parábola tem concavidade para cima e quando a abertura está voltada para baixo dizemos que tem concavidade para baixo.
Uma das formas de saber se uma parábola tem concavidade para cima ou para baixo, é por meio do coeficiente a da função quadrática.
- Se a for um número positivo (a > 0), a parábola tem concavidade para cima.
- Se a for um número negativo (a < 0), a parábola tem concavidade para baixo.
Vértice da parábola
O vértice da parábola é o ponto onde a curva muda de sentido. Em uma parábola com concavidade para cima, ele é o ponto mais baixo do gráfico, e em uma parábola com concavidade para baixo, ele é o ponto mais alto.
Podemos saber onde está o vértice de uma parábola calculando as coordenadas x e y desse ponto.
As coordenadas do vértice da parábola são:
Sendo
o discriminante.
Ponto de máximo e ponto de mínimo
Uma parábola possui um ponto de máximo ou um ponto de mínimo, nunca os dois.
Se a parábola tiver concavidade para cima, o vértice é o ponto de mínimo. Assim, o ponto de mínimo é o ponto mais baixo do gráfico. De todos os pontos da parábola, o ponto de mínimo possui a menor coordenada y.
Mas se a parábola tiver concavidade para baixo, o vértice é o ponto de máximo. Portanto, o ponto de máximo é o ponto mais alto do gráfico. De todos os pontos da parábola, o ponto de máximo possui a maior coordenada y.
Exemplo
Vamos analisar a concavidade da função f(x) = 2x² – 5.
Temos a = 2, b = 0 e c = -5.
Como a é um valor positivo (a > 0), então, a parábola y = 2x² – 5 tem concavidade para cima.
Assim, o vértice é um ponto de mínimo da função com coordenadas:
Vértice: V(0, -5) → ponto de mínimo.
Veja a representação gráfica da função f(x) = 2x² – 5:
Você também pode se interessar:


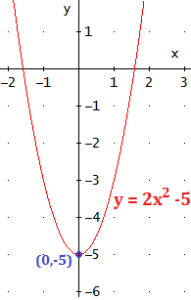
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.