Conjuntos numéricos
Os conjuntos numéricos são conjuntos de números com características semelhantes. Temos conjuntos dos naturais, dos inteiros, dos racionais, dos irracionais e dos reais. Aprenda sobre cada um desses conjuntos.
Os principais conjuntos numéricos são:
- Conjunto dos números naturais;
- Conjunto dos números inteiros;
- Conjunto dos números racionais;
- Conjunto dos números irracionais;
- Conjunto dos números reais.
Vamos aprender sobre cada um deles?!
Conjunto dos números naturais
Os números naturais são os números que utilizamos para contar objetos e seres, como pessoas, livros, carros, animais, dias do ano, etc.
O conjunto dos números naturais é representado pela letra e pode ser expresso da seguinte forma:
Conjunto dos números inteiros
O números inteiros são todos os números naturais e, também, todos os números naturais considerando sinal negativo.
O conjunto dos números inteiros é representado pela letra e pode ser expresso como:
Conjunto dos números racionais
Os números racionais são todos os números que podem ser escritos em forma de fração, em que o denominador seja um número inteiro e o denominador também, mas diferente de zero.
O conjunto dos números racionais é representado pela letra e pode ser representado como:
Exemplos de números racionais:
Observações:
1 – Todo número inteiro é um número racional
2 – Todo número decimal finito é um número racional
Um número decimal finito é aquele que possui um número finito de casas decimais. Exemplos:
- 2,1
- 0,29
- 14,508
3 – Toda dízima periódica é um número racional
As dízimas periódicas são números decimais infinitos, mas com um padrão de repetição. Exemplos:
- 0,9999999…
- 2,15151515…
- 10,815815815…
Conjunto dos números irracionais
Os números irracionais são todos os números que tem representação decimal infinita não periódica, ou seja, sem um padrão de repetição nas casas decimais.
Por exemplo: 0,0371328….; 12,4529023…; ;
, são números irracionais.
O conjunto dos números irracionais é representado pela letra .
Conjunto dos números reais
Os números reais são todos os números racionais e todos os números irracionais.
O conjunto dos números reais é representado pela letra e pode ser descrito como a união entre o conjunto dos racionais (
) e o conjunto dos irracionais (
).
Subconjuntos
Podemos ter subconjuntos dos conjuntos vistos anteriormente. Vamos considerar o conjunto dos números inteiros para mostrar a notação utilizada. Para os demais conjuntos, a notação é a mesma.
– Conjunto sem o número zero:
– Conjunto contendo apenas os números maiores ou iguais a zero:
– Conjunto contendo apenas os números maiores que zero:
– Conjunto contendo apenas os números menores ou iguais a zero:
– Conjunto contendo apenas os números menores que zero:
Relação entre os conjuntos numéricos
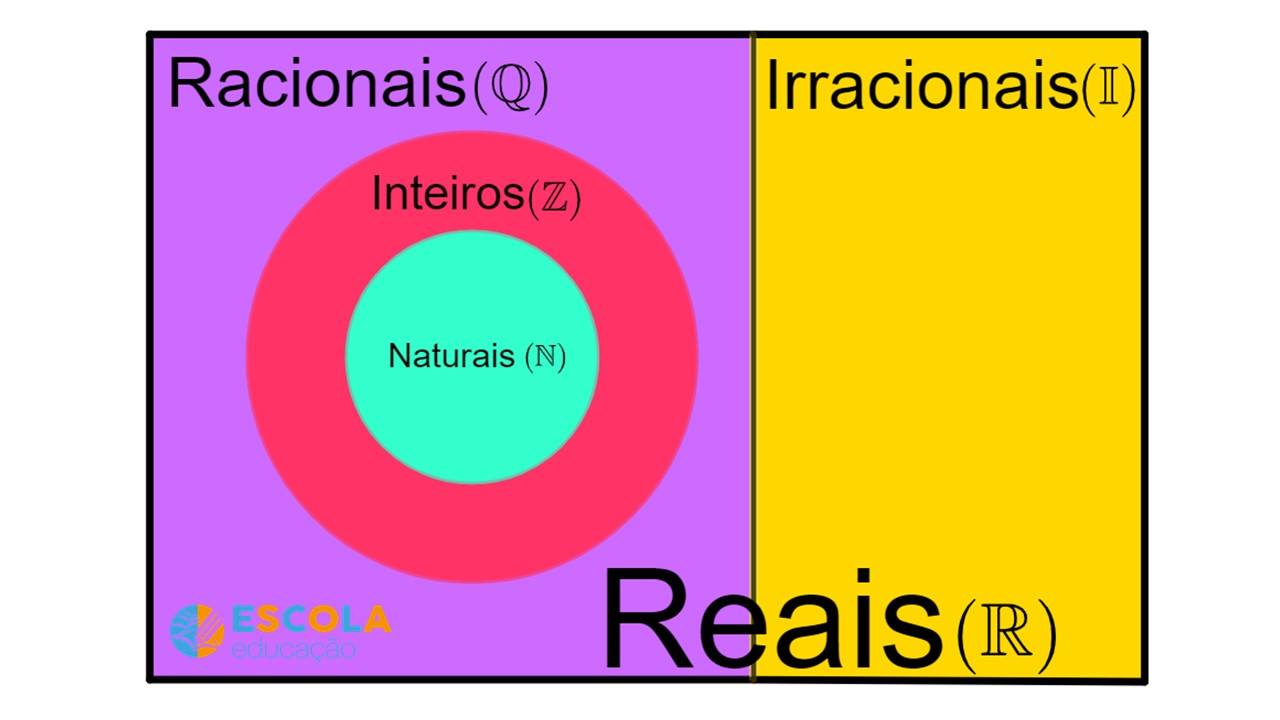
Os conjuntos estão relacionados da seguinte forma:
- O conjunto dos naturais (
) é um subconjunto dos números inteiros (
);
- O conjunto dos inteiros (
) é um subconjunto dos números racionais (
);
- O conjunto dos racionais (
) é um subconjunto dos números reais (
);
- O conjunto dos irracionais (
) é um subconjunto dos números reais (
);
- O conjunto dos racionais (
) e dos irracionais (
) não tem nenhum número em comum.
Veja a representação dos conjuntos e as relações entre eles:
Veja também: História e origem dos números que utilizamos hoje em dia

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.