Determinante de uma matriz
Aprenda a calcular o determinante de matrizes de ordem 2 e 3 pelo método da diagonal.
O determinante de uma matriz é um número que pode ser obtido para matrizes quadradas, que são matrizes com mesmo número de linhas e colunas. O cálculo do determinante é útil, por exemplo, em problemas envolvendo sistemas de equações.
Existem algumas formas de calcular o determinante de uma matriz, nesse post vamos mostrar como calcular esse valor numérico pelo método de Sarrus, também conhecido por método da diagonal.
Em uma matriz de ordem 1 x 1, o determinante é o único elemento da matriz. Então, vamos ver como encontrar o determinante para matrizes de ordens 2 e 3.
Determinante de uma matriz 2 x 2
Vamos calcular o determinante de uma matriz A de ordem 2 x 2.
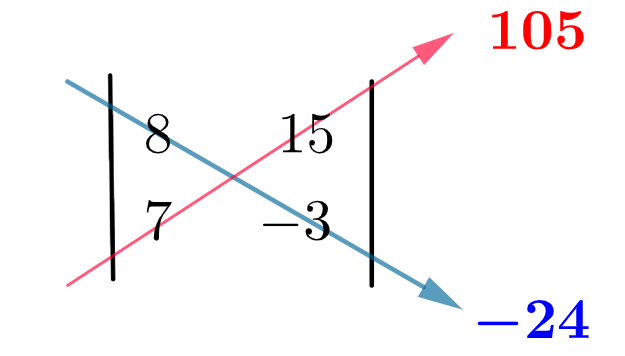
Primeiro, calculamos o produto entre os valores da diagonal principal (cor azul) e o produto entre os valores da diagonal secundária (cor vermelha). Veja que 8 x (-3) = -24 e 7 x 15 = 105.
Por último, fazemos a subtração entre esses valores obtidos:
-24 – 105 = – 129
Então, o determinante da matriz A é igual a -129.
Determinante de uma matriz 3 x 3
Vamos calcular o determinante de uma matriz A de ordem 3 x 3.
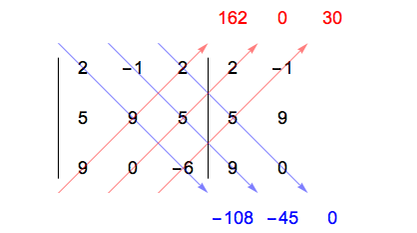
Primeiro, devemos escrever a matriz e repetir a primeira e a segunda coluna:
Depois, calculamos a multiplicação dos elementos de cada uma das diagonais da matriz, as principais (cor azul) e as secundárias (cor vermelha). Por exemplo, veja que 2 x 9 x (-6) = -108.
Por fim, somamos todos esses valores, mas colocando um sinal negativo nos valores das diagonais secundárias (cor vermelha). Observe que colocamos o sinal negativo antes dos parênteses.
-108 + (-45) + 0 – (162 + 0 + 30) = -345
Fazendo o cálculo, obtemos o determinante da matriz A, que é igual a -345.
Você também pode se interessar:
- Regra de sinais
- Números complexos
- Lista de exercícios de expressões numéricas
- Funções trigonométricas – Seno, cosseno e tangente

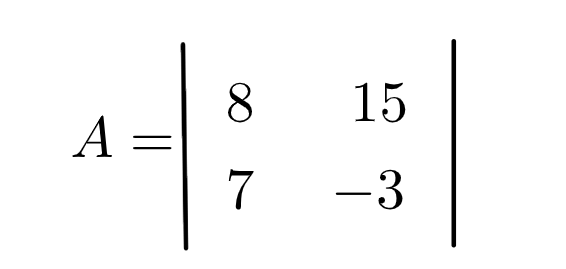
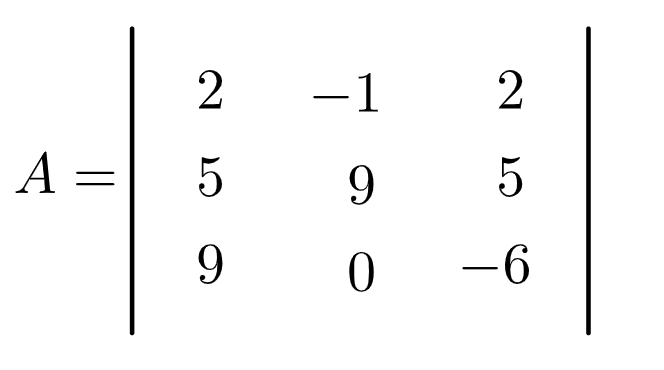
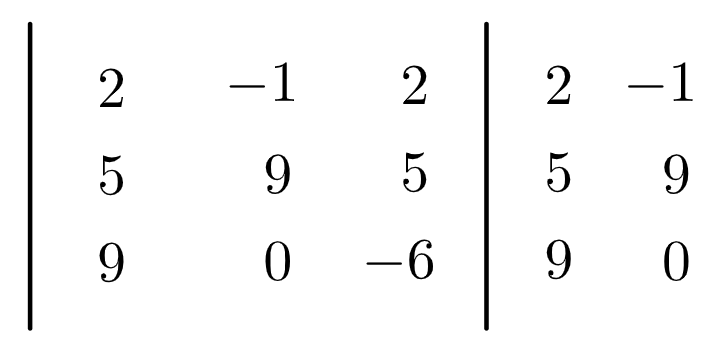
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.