Diagonal do bloco retangular
A diagonal do bloco retangular pode ser determinada por uma fórmula que só depende do comprimento, largura e altura do bloco.
A diagonal do bloco retangular é o segmento de reta que liga dois vértices que estão em faces distintas, ou seja, a diagonal do bloco sempre deve passar pelo interior da figura.
O bloco retangular, que também é chamado de paralelepípedo retângulo, é um tipo de prisma reto, cujas faces são todas retangulares.
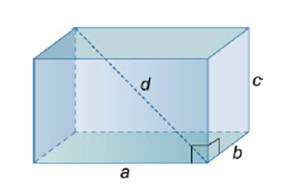
As dimensões de um bloco retangular são: comprimento (a), largura (b) e altura (c). A partir dessas dimensões, podemos determinar a medida da sua diagonal (d).
Fórmula da diagonal do bloco retangular
A fórmula para calcular a medida da diagonal do bloco retangular é:
Em que:
- a: comprimento do bloco;
- b: largura do bloco;
- c: altura do bloco.
Exemplo:
Determine a medida da diagonal do bloco retangular com as dimensões especificadas na figura abaixo.
Temos: a = 5 m, b = 4m e c = 2,5 m. Vamos aplicar esses valores na fórmula:
Demonstração da fórmula
A demonstração de que essa fórmula é verdadeira é feita a partir do Teorema de Pitágoras.
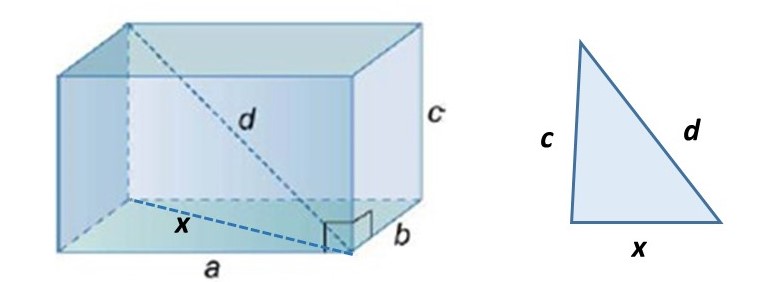
Observe na figura abaixo que a diagonal d é a hipotenusa de um triângulo retângulo de catetos c e x, sendo c a altura e x uma medida, por enquanto, desconhecida.
Pelo teorema de Pitágoras, temos que:
Aplicando a raiz em ambos os lados da equação, temos que:
A ideia é obter uma fórmula que só dependa das dimensões a, b e c do bloco retangular. Para isso, veja que x é a diagonal do retângulo de dimensões a e b, que é uma das faces do bloco. Então, temos que:
Ou, ainda, de modo equivalente, elevando ao quadrado ambos os lados:
Substituindo x² na fórmula da diagonal, temos que:
Você também pode se interessar:
- Diagonal do quadrado e do retângulo
- Medidas de volume e capacidade
- Perímetro de figuras planas
- Planificação de sólidos geométricos
- A esfera na geometria espacial


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.