Perímetro de figuras planas
Perímetro é uma medida de figuras geométricas planas, corresponde à medida do contorno. Veja as fórmulas de perímetro!
Perímetro é a medida do contorno das figuras geométricas planas. Nas figuras formadas apenas por segmentos de reta, o perímetro é calculado a partir da soma das medidas de todos os lados.
Veja, a seguir, como calcular o perímetro de figuras planas.
Perímetro de figuras planas
As figuras planas se diferenciam em relação ao formato e à quantidade de lados e suas medidas. Por isso, apesar do perímetro ser sempre a medida do contorno, a forma de calculá-lo pode variar entre as figuras.
Mas não se preocupe, pois, para as figuras planas mais comuns, existem fórmulas para o cálculo do perímetro. Confira!
O quadrado é um polígono de quatro lados iguais, ou seja, todos têm o mesmo tamanho. Assim, o perímetro do quadrado é obtido multiplicando a medida do lado por 4.
: medida do lado do quadrado.
O retângulo é um polígono de quatro lados, mas apenas os lados opostos têm a mesma medida. O perímetro do retângulo é obtido pela seguinte fórmula:
Em que:
b: medida da base do retângulo;
h: altura do retângulo.
O triângulo é um polígono de três lados, que podem ter medidas iguais ou diferentes. De modo geral, o perímetro do triângulo é obtido somando as três medidas dos lados.
a , b e c: medidas dos lados do triângulo.
Se o triângulo for equilátero, isto é, todos os lados iguais o perímetro é obtido multiplicando a medida do lado por 3.
O trapézio é um polígono de quatro lados, sendo dois lados paralelos e dois lados não paralelos. Os lados paralelos são chamados de bases, uma maior e outra menor.
O perímetro do trapézio é calculado a partir da fórmula abaixo:
Em que:
B: medida da base maior;
b: medida da base menor;
: medidas dos lados não paralelos.
O losango é um polígono de quatro lados iguais e a fórmula do perímetro é igual a do quadrado:
: medida do lado do losango.
Vale ressaltar que a diferença entre quadrado e losango está na medida dos ângulos internos. No quadrado, todos os ângulos internos medem exatamente 90°, já no losango, não.
O círculo é uma figura plana classificada como não polígono, pois não é formado por segmentos de reta. Assim, o seu perímetro é calculado de uma forma diferente.
A fórmula do perímetro do círculo é:
Em que:
: raio do círculo.
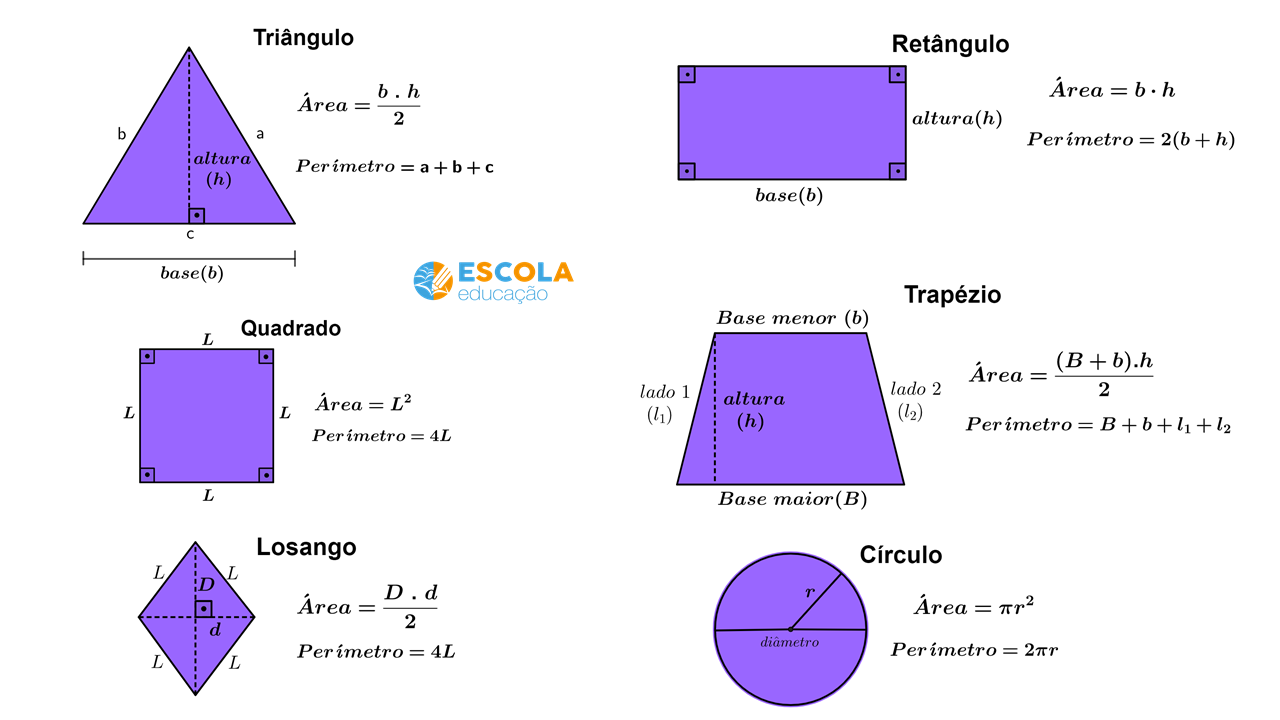
Fórmula do perímetro e área de figuras planas
Veja a seguir um quadro de resumo com todas as fórmulas de perímetro e, também, de área de figuras planas.
Clique aqui para baixar essa imagem em PDF!
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.