Lista de exercícios de gráficos

Confira uma lista de exercícios resolvidos sobre gráficos e fique mais perto se dar bem nas provas de matemática!

Por Elainy Marciano Publicado em 24/08/2020 - 22:37

Nas provas de concurso e vestibular, muitas questões são apresentadas com gráficos e os candidatos precisam estar preparados para interpretá-los e extrair as informações necessárias para obter a resposta correta.

Pensando nisso, preparamos uma lista de exercícios de gráficos, todos com resolução e gabarito para que você possa treinar e ficar mais perto de se dar bem nas provas de matemática!

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Lista de exercícios de gráficos

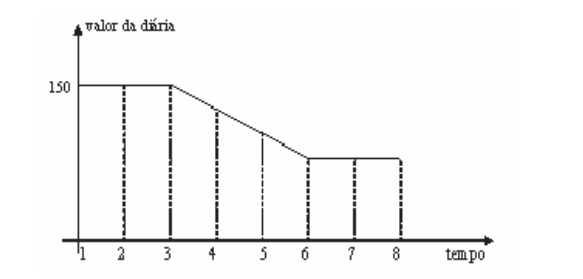
Questão 1. (Enem 2009) Uma pousada oferece pacotes promocionais para atrair casais a se hospedarem por até oito dias. A hospedagem seria em apartamento de luxo e, nos três primeiros dias, a diária custaria R$ 150,00, preço da diária fora da promoção. Nos três dias seguintes, seria aplicada uma redução no valor da diária, cuja taxa média de variação, a cada dia, seria de R$ 20,00. Nos dois dias restantes, seria mantido o preço do sexto dia. Nessas condições, um modelo para a promoção idealizada é apresentado no gráfico a seguir, no qual o valor da diária é função do tempo medido em número de dias.

De acordo com os dados e com o modelo, comparando o preço que um casal pagaria pela hospedagem por sete dias fora da promoção, um casal que adquirir o pacote promocional por oito dias fará uma economia de:

A) R$ 90,00.
B) R$ 110,00.
C) R$ 130,00.
D) R$ 150,00.
E) R$ 170,00.

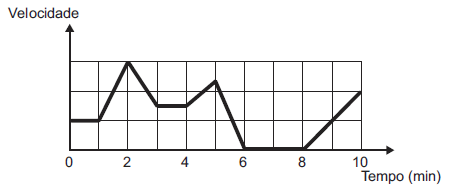
Questão 2. (Enem 2017) Os congestionamentos de trânsito constituem um problema que aflige, todos os dias, milhares de motoristas brasileiros. O gráfico ilustra a situação, representando, ao longo de um intervalo definido de tempo, a variação da velocidade de um veículo durante um congestionamento.

Quantos minutos o veículo permaneceu imóvel ao longo do intervalo de tempo total analisado?

A) 4.
B) 3.
C) 2.
D) 1.
E) 0.

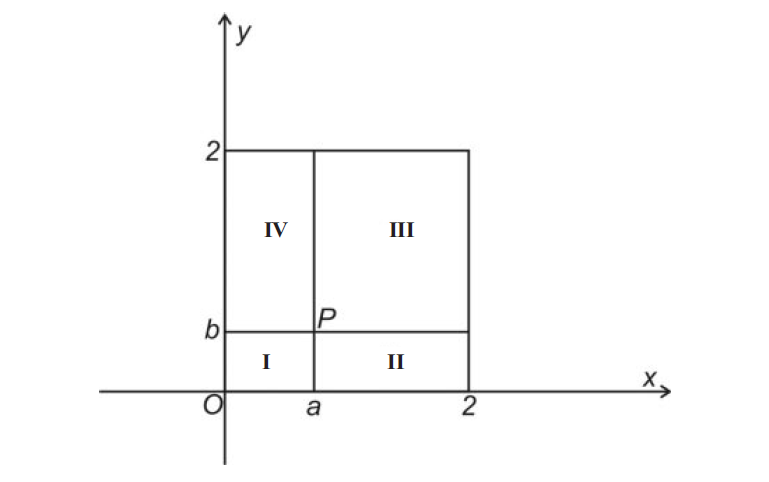
Questão 3. (UFMG 2007) Seja P = (a,b) um ponto no plano cartesiano tal que 0 < a < 1 e 0 < b < 1. As retas paralelas aos eixos coordenados que passam por P dividem o quadrado de vértices (0,0), (2,0), (0,2) e (2,2) nas regiões I, II, III e IV, como mostrado nesta figura:

Considere o ponto $\mathrm{Q = (\sqrt{a^2 + b^2},ab)}$ . Então, é CORRETO afirmar que o ponto $\mathrm{Q}$ está na região:

A) I.
B) II.
C) III.
D) IV.

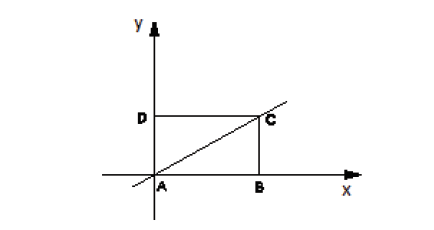
Questão 4. (PUC – RIO 2014) O retângulo ABCD tem um lado sobre o eixo x e um lado sobre o eixo y, como mostra a figura. A equação da reta que passa por A e por C é $\mathrm{y=\frac{2}{3}x}$ , e a medida do lado AB é 6. A área do triângulo ABC é:

A) 10.
B) 11.
C) 24.
D) 12.
E) 6.

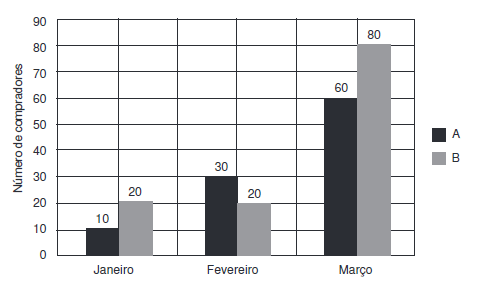
Questão 5. (Enem 2013) Uma loja acompanhou o número de compradores de dois produtos, A e B, durante os meses de janeiro, durante os meses de janeiro, fevereiro e março de 2012. Com isso, obteve este gráfico:

A loja sorteará um brinde entre os compradores do produto A e outro brinde entre os compradores do produto B.

Qual a probabilidade de que os dois sorteados tenham feito suas compras em fevereiro de 2012?

A) $\frac{1}{20}$

B) $\frac{3}{242}$

C) $\frac{5}{22}$

D) $\frac{6}{25}$

E) $\frac{7}{15}$

Resolução da questão 1

Fora da promoção, a diária custa R$ 150,00, então, um casal que se hospeda por 7 dias irá pagar R$ 1050,00, pois:

150 × 7 = 1050

Já um casal que se hospeda por 8 dias, dentro da promoção, irá pagar R$ 960,00, pois:

(150 × 3) + 130 + 110 + (90 × 3) = 960

Calculando a diferença entre 1050 e 960, vemos que o casal que adquiriu o pacote promocional fará uma economia de R$ 90,00.

Alternativa correta: A.

Resolução da questão 2

Observando o gráfico, podemos notar que o veículo permaneceu imóvel do minuto 6 ao minuto 8, que é quando a velocidade (eixo vertical) é igual a 0.

Portanto, o veículo permaneceu imóvel por 2 minutos.

Alternativa correta: C.

Resolução da questão 3

A abscissa do ponto Q é a hipotenusa (c) do triângulo retângulo de catetos a e b:

$\mathrm{c = \sqrt{a^2 + b^2}$

A hipotenusa de um triângulo retângulo é sempre maior que qualquer um dos catetos, então, temos c > a, portanto, a abscissa do ponto Q é um valor maior que a.

Agora, vamos ver sobre a ordenada do ponto Q. Temos 0 < a < 1 e 0 < b < 1 e queremos saber o intervalo de ab.

Se b pudesse ser 0, então, teríamos ab = 0, e se b pudesse ser 1, teríamos ab = a e poderíamos concluir que 0 $\leq$ ab $\leq$ a.

Contudo, temos 0 < b < 1, o que implica que 0 < ab < a. De forma análoga, temos 0 < a < 1, o que implica que 0 < ab < b.

Portanto, a ordenada do ponto Q é um valor menor que b. Assim, o ponto Q está na região II do gráfico.

Alternativa correta: B

Resolução da questão 4

Podemos calcular a área do triângulo a partir da medida da base e da altura.

Sabemos que a medida do lado AB é igual a 6, então, já temos a medida da base.

Resta-nos calcular a medida da altura, que, neste caso, corresponde a ordenada do ponto C (6,y).

Como C pertence a reta $\mathrm{y=\frac{2}{3}x}$ , basta substituir x por 6 para determinar y.

$\mathrm{y=\frac{2}{3}\cdot 6 = 4}$

Logo, a altura é igual a 4.

$A = \frac{6 \cdot 4}{2} = 12$

Alternativa correta: D.

Resolução da questão 5

Observando o gráfico, vemos que 30 pessoas compraram o produto A em fevereiro e que 10 + 30 + 60 = 100 pessoas compraram o produto A no período todo.

Assim, para o produto A, a probabilidade de que o sorteado tenha feito a compra em fevereiro é:

$P_A = \frac{30}{100} =\frac{3}{10}$

Além disso, notamos que 20 pessoas compraram o produto B em fevereiro e que 20 + 20 + 80 = 120 pessoas compraram o produto A no período todo.

$P_B = \frac{20}{120} =\frac{2}{12} = \frac{1}{6}$

Multiplicando essas duas probabilidades, determinamos a probabilidade de que os dois sorteados tenham comprado em fevereiro:

$P_A\cdot P_B = \frac{3}{10}\cdot \frac{1}{6} = \frac{1}{20}$

Alternativa correta: A.

Você também pode se interessar:

Gráficos