Função quadrática
Entenda o que é uma função quadrática, como é o gráfico desse tipo de função, quais são suas propriedades e como encontrar as suas raízes ou zeros.
A função quadrática ou função do 2° grau é uma função com a seguinte forma:
Em que são números reais e
.
Observe que o termo quadrático sempre deve aparecer em uma função quadrática, já que
. No entanto, nem sempre teremos os termos
e
, uma vez que
podem ser iguais a zero.
Vamos ver alguns exemplos de função quadrática:
a) → Temos
b) → Temos
c) → Temos
d) → Temos
d) → Temos
Representação gráfica
O gráfico de uma função quadrática é sempre uma parábola, que pode ser traçada quando atribuímos valores para x e calculamos y = f(x), determinando vários pares ordenados (x, y).
Além disso, existem algumas propriedades da função quadrática que podem nos ajudar na construção do seu gráfico.
Concavidade da parábola
O valor da constante na função quadrática é o que determinará a concavidade da parábola. Se
for um valor positivo, então a parábola tem concavidade para cima e se
for um valor negativo, a parábola tem concavidade para baixo.

Vértice da parábola
O vértice de uma parábola é o ponto onde a curva muda o sentido, torna-se crescente quando é côncava para cima ou torna-se decrescente, quando é côncava para baixo.
Podemos encontrar as coordenadas desse ponto da seguinte forma:
Onde é o discriminante.
Raízes ou zeros de uma função quadrática
A raízes ou zeros de uma função quadrática são os pontos onde o gráfico intercepta o eixo x. Para encontrar esses valores devemos encontrar as soluções da seguinte equação do 2° grau:
Uma das formas de encontrar os valores de x que tornam essa igualdade verdadeira, é utilizando a fórmula de Bhaskara:
Em que:
Além disso, também podemos saber em qual ponto o gráfico intercepta o eixo y. Para isso, só temos que calcular y = f(0), isto é, substituir x por 0 e calcular o valor de y correspondente.
Exemplo
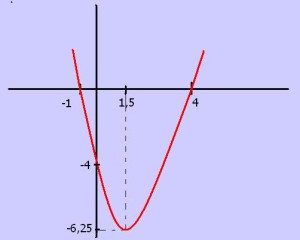
Vamos analisar a função quadrática:
Temos .
Concavidade:
Voltada para cima, pois .
Vértice:
Assim, o vértice é o ponto (1,5 ; -6,25).
Raízes:
Logo, a parábola intercepta o eixo x nos valores -1 e 4.
Ponto de Intercepto no eixo y:
então:
Portanto, a parábola intercepta o eixo y no valor -4.
Você também pode se interessar:
- Função injetora
- Domínio, contradomínio e imagem
- Exercícios de função do primeiro grau (função afim)
- Funções trigonométricas – Seno, cosseno e tangente

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.