Como fazer o gráfico da função do segundo grau
O gráfico de uma função do 2° grau é uma parábola. Aprenda a encontrar os pontos notáveis da parábola para construir o gráfico.
O gráfico de uma função y = f(x) corresponde a representação, no plano cartesiano, dos pares ordenados (x,y) que pertencem à função. Para uma função do 2° grau, o gráfico corresponde a uma parábola.
Podemos construir o gráfico da função do 2° grau, atribuindo uma porção de valores para x, substituindo na função e calculando o valor de y correspondente. Em seguida, marcamos cada um dos pares ordenados (x,y) que calculamos e traçamos a parábola.
No entanto, se soubermos apenas a concavidade e alguns pontos-chaves da parábola, já podemos traçar o gráfico da função do 2° grau.
Esses pontos-chaves da parábola também são chamados de pontos notáveis, eles são: o vértice e os pontos de intersecção com os eixos x e y.
Gráfico de uma função do 2° grau
Para explicar como fazer o gráfico de uma função do 2° grau, vamos mostrar alguns exemplos.
Exemplo 1) Construir o gráfico da seguinte função do 2° grau:
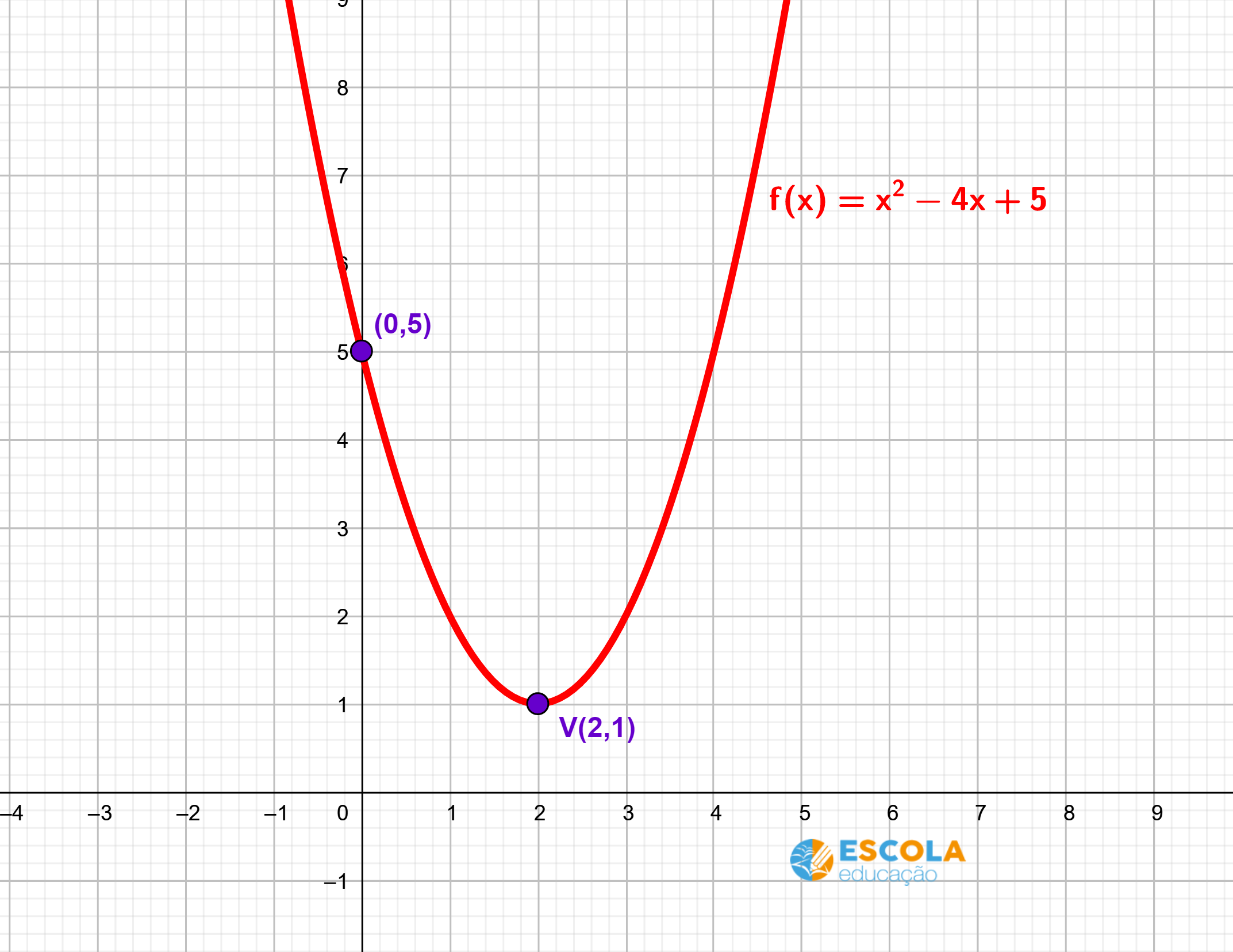
f(x) = x² – 4x + 5
Coeficientes da função:
Temos a = 1, b = -4 e c = 5.
Concavidade da parábola:
Como o coeficiente a é um número positivo, então a concavidade é para cima.
Intercepto com o eixo x:
Como , não existem raízes reais para essa função. Assim, a parábola não intercepta o eixo x.
Intercepto com o eixo y:
f(0) = 0² – 4.0 + 5 = 5
Logo, o ponto de intercepto da parábola com o eixo y é o ponto (0,5).
Vértice da parábola:
As coordenadas do vértice da parábola podem ser calculadas da seguinte forma:
Assim, o vértice da parábola é o ponto V(2,1).
Para fazer o gráfico, marcamos os pontos (0,5) e (2,1) e traçamos uma parábola côncava para cima com vértice no ponto (2,1) e passando pelo ponto (0,5).
Exemplo 2) Construir o gráfico da seguinte função do 2° grau:
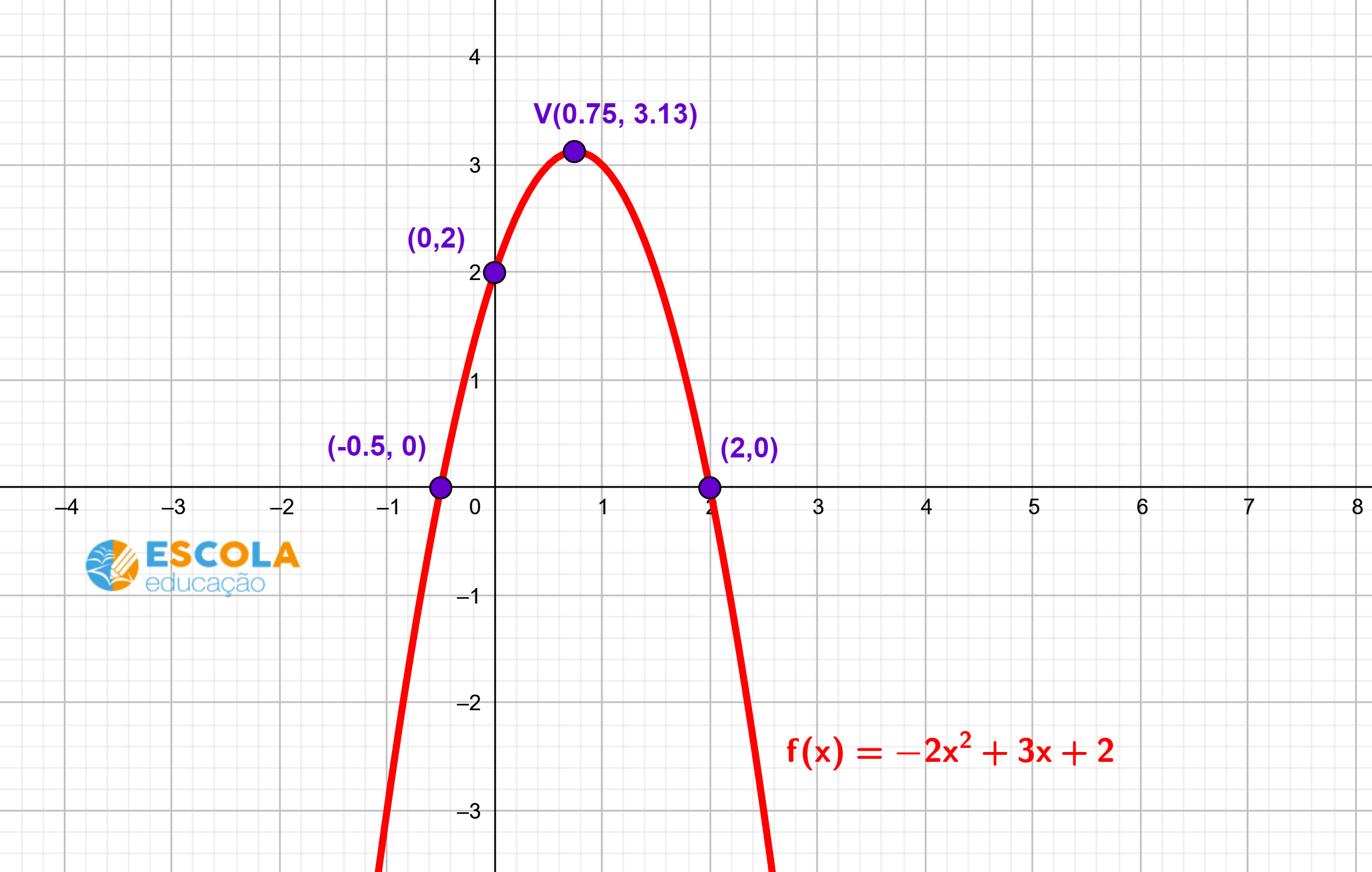
f(x)= -2x² + 3x + 2
Coeficientes da função:
Temos a = -2, b = 3 e c = 2.
Concavidade da parábola:
Como o coeficiente a é um número negativo, então a concavidade é para baixo.
Intercepto com o eixo x:
Como , existem duas raízes reais diferentes para essa função. Assim, a parábola intercepta o eixo x em dois pontos.
Para encontrar esses pontos, podemos utilizar a fórmula de Bhaskara.
De onde obtemos: e
.
Assim, a parábola intercepta o eixo x nos pontos (-0,5, 0) e (2,0).
Intercepto com o eixo y:
f(0) = -20² + 3.0 + 2 = 2
Logo, o ponto de intercepto da parábola com o eixo y é o ponto (0,2).
Vértice da parábola:
Assim, o vértice da parábola é o ponto V(0,75; 3,13).
Para fazer o gráfico, marcamos os pontos (-0,5; 0), (2,0), (0,2) e (0,75; 3,13) e traçamos uma parábola côncava para baixo com vértice no ponto (0,75; 3,13) e passando pelos pontos (-0,5; 0), (2,0) e (0,2).
Você também pode se interessar:
- Sinais de uma equação do 2° grau
- Função injetora
- Função do primeiro grau (função afim)
- Exercícios de função do primeiro grau (função afim)

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.