Multiplicação de frações

Saiba como multiplicar frações, o que essa operação significa e como utilizar a técnica do cancelamento na multiplicação de frações.

Por Elainy Marciano Publicado em 09/06/2020 - 15:26

As frações são um tipo de numeral utilizado para representar partes de um todo e uma das operações matemáticas que podemos realizar com elas é a multiplicação.

Vamos ver como fazer esse tipo de cálculo entre frações?

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Como fazer a multiplicação de frações

Para entender como fazer a multiplicação de frações, a primeira coisa que devemos saber é que o resultado da multiplicação entre duas frações, é uma fração.

Nessa fração resultante, o numerador é obtido através do produto entre os numeradores das frações dadas, e o denominador, através do produto entre os denominadores.

Em resumo:

Para multiplicar duas frações, basta multiplicar os numeradores e multiplicar os denominadores, obtendo uma nova fração como resultado.

Exemplos:

a) $\frac{1}{3} \times \frac{2}{5}$

$\frac{1}{3} \times \frac{2}{5} = \frac{1 \times 2}{3 \times 5} = \boldsymbol{\frac{2}{15}}$

b) $\frac{3}{11} \times \frac{2}{9}$

$\frac{3}{11} \times \frac{2}{9} = \frac{3 \times 2}{11 \times9} = \mathbf{\frac{6}{99}}$

Como fazer a multiplicação de um número natural por uma fração

A multiplicação entre um número natural qualquer e uma fração é bem semelhante à multiplicação entre duas frações.

Qualquer número natural pode ser visto como uma fração de denominador igual a 1. Veja:

$1 = \frac{1}{1}$

$2 = \frac{2}{1}$

$10 = \frac{10}{1}$

Assim, sempre que formos multiplicar um número natural por uma fração, basta considerarmos o número 1 como denominador e fazermos a multiplicação entre duas frações.

Exemplo: $\frac{8}{3} \times 5$

$\frac{8}{3} \times 5 = \frac{8}{3} \times \frac{5}{1} = \mathbf{\frac{40}{3}}$

Simplificação na multiplicação de frações

Quando lidamos com frações, é sempre preferível que elas estejam em sua forma simplificada ou irredutível.

Na multiplicação de frações, podemos simplificar a fração resultante ou utilizar a técnica do cancelamento antes de realizarmos o produto entre os termos.

Exemplo: $\frac{3}{7} \times \frac{9}{3}$

Vamos resolver de duas formas:

1ª) multiplicando e depois simplificando:

$\frac{3}{7} \times \frac{9}{3} = \frac{3\times9}{7 \times 3} = \frac{27}{21} = \mathbf{\frac{9}{7}}$

2ª) utilizando a técnica do cancelamento:

$\frac{\cancel{3}}{7} \times \frac{9}{\cancel{3}} = \frac{1}{7} \times \frac{9}{1} = \mathbf{\frac{9}{7}}$

Significado da multiplicação de frações

Muitos problemas que podem ser resolvidos apenas com uma simples multiplicação de frações, podem parecer difíceis quando não há o entendimento do significado dessa multiplicação.

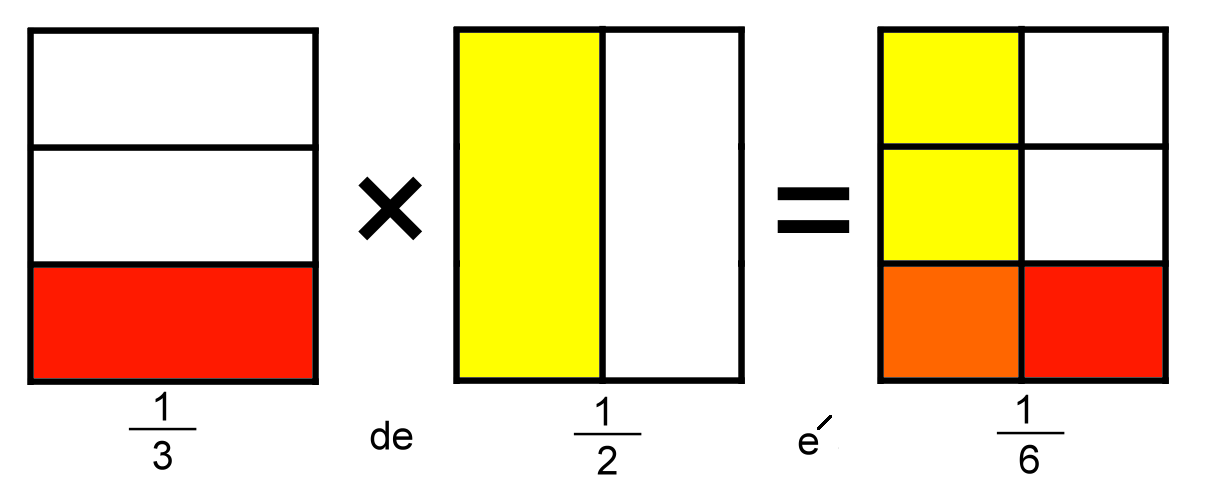
Para compreender o que significa multiplicar duas frações, observe a representação geométrica da multiplicação entre 1/3 e 1/2.

Pela figura, podemos ver que calcular 1/3 x 1/2 é o mesmo que saber quanto é 1/3 de 1/2.

Veja que 1/2 corresponde a parte amarela do retângulo, então, para saber quanto é 1/3 dessa parte amarela, basta dividir a parte amarela em três partes e considerar apenas uma dessas partes.

No retângulo, essa parte corresponde ao quadrado laranjado, que representa 1/6 dele.

Agora que já sabemos o que significa a multiplicação de frações, vamos ver o exemplo de um problema que pode ser solucionado com essa simples operação entre frações.

Exemplo de problema envolvendo multiplicação de frações:

Em uma escola, 1/3 dos alunos têm menos de 10 anos. Entre esses alunos, 3/5 deles usam óculos. Que fração dos alunos dessa escola tem menos de 10 anos e usam óculos?

Queremos saber quanto é $\frac{3}{5}$ de $\frac{1}{3}$ , ou seja $\frac{3}{5} \times \frac{1}{3}$ .