O que são ângulos congruentes?

Ângulos congruentes são dois ângulos que possuem a mesma medida em graus, ou seja, a abertura formada é a mesma.

O símbolo matemático usado para indicar que dois ângulos são congruentes é ≅.

Exemplo:

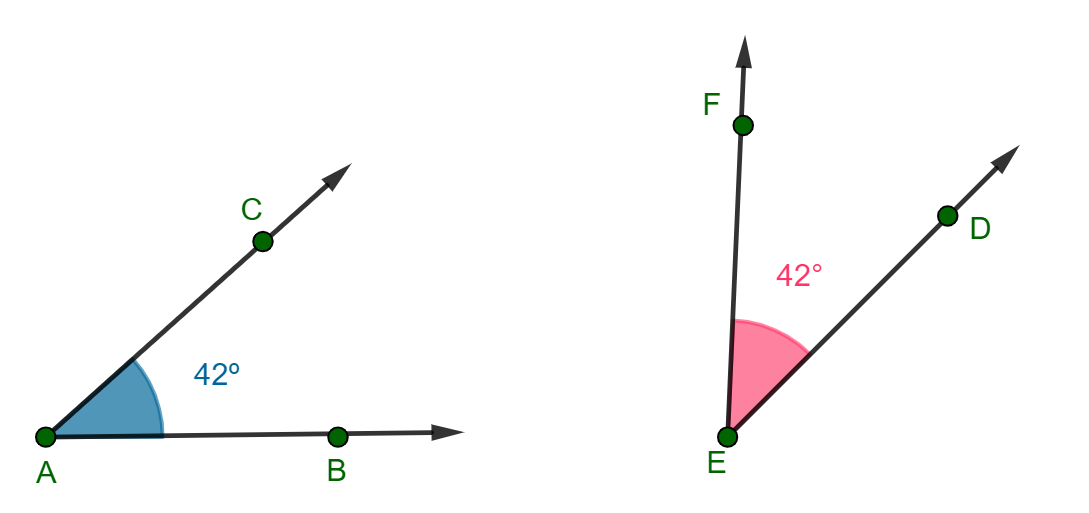
Veja que o ângulo  mede 42° e o ângulo  também mede 42°, ou seja:

Portanto, eles são congruentes:

Como você pode ver, a congruência de dois ângulos não tem a ver com a posição deles no plano ser a mesma, eles podem estar posicionados de forma diferente e serem congruentes, como é o caso dos ângulos do exemplo.

Além disso, veja que quando comparamos as medidas dos ângulos congruentes usamos o símbolo de igualdade (=), pois as medidas são iguais. O símbolo ≅ só é usado quando nos referimos aos próprios ângulos.

Exercício:

Os ângulos  e  são congruentes. Sabendo que  e que , descubra o valor de .

Resolução:

Se os ângulos são congruentes, então, suas medidas são iguais:

Isolando  na equação, temos que:

Você também pode se interessar:

• Ângulos notáveis
• Bissetriz
• Mediatriz
• Ângulos colaterais internos e externos
• Congruência de formas geométricas