Ângulos notáveis

Aprenda o que são e quais são os principais ângulos notáveis para facilitar seus estudos de trigonometria! Veja uma tabela de ângulos notáveis e as demonstrações do seno e cosseno.

Por Elainy Marciano Publicado em 16/07/2020 - 16:15

Os ângulos notáveis são os ângulos mais utilizados em trigonometria: 0°, 30°, 45°, 60° e 90°.

Por isso, é comum precisar do valor das funções trigonométricas, seno, cosseno e tangente, desses ângulos.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Veja, a seguir, uma tabela com os ângulos notáveis. Ela será muito útil na hora dos estudos!

Tabela de ângulos notáveis

Na tabela de ângulos notáveis são apresentados os valores do seno, cosseno e tangente dos ângulos 0°, 30°, 45°, 60° e 90°.

Essa é uma daquelas tabelas para você ter sempre em mãos na hora de fazer exercícios de trigonometria ou até mesmo decorar, já que são valores muito utilizados.

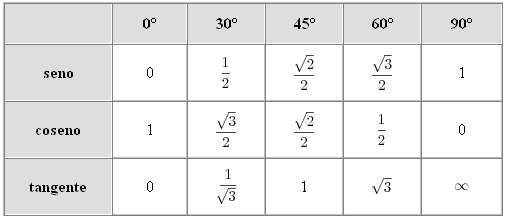
Para saber o valor do seno de 30°, por exemplo, basta consultar a 1ª linha e 2ª coluna da tabela: seno de 30° = 1/2.

Mas de onde vem esses valores? Veja, a seguir, a demonstração dos valores do seno e cosseno de 30°, 45° e 60°.

Seno e o cosseno de 30° e 60°

Para demonstrar que os valores do seno e cosseno de 30° e 60° são os valores apresentados na tabela anterior, basta considerar um triângulo que tenha como ângulos internos esses dois ângulos notáveis.

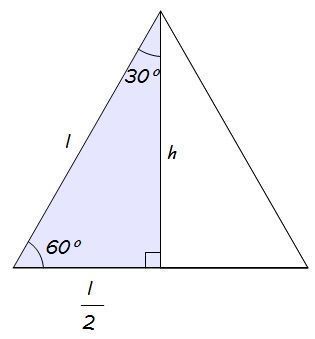
Assim, consideramos um triângulo equilátero de lado l qualquer. Uma propriedade dos triângulos equiláteros, é que os ângulos internos são todos iguais e medem, cada um, 60°.

Além disso, traçando o segmento h que corresponde à altura de um triângulo equilátero, obtemos dois triângulos congruentes, cada um com ângulos internos de 30°, 60° e 90° e lados $\dpi{120} l$ , $\dpi{120} \frac{l}{2}$ e $\dpi{120} h$ .

Observe que cada um dos triângulos é um triângulo retângulo. Assim, podemos aplicar o teorema de Pitágoras, considerando hipotenusa igual a $\dpi{120} l$ e catetos $\dpi{120} h$ e $\dpi{120} \frac{l}{2}$ e mostrar que a altura de um triângulo equilátero é dada por:

$\dpi{120} h = \frac{l\sqrt{3}}{2}$

Agora, os três lados do triângulo retângulo dependem apenas de um único valor desconhecido, o valor $\dpi{120} l$ .

Vamos aplicar as relações de seno e cosseno de cada um dos ângulos.

$\dpi{120} seno = \frac{cateto\: oposto}{hipotenusa}$ e $\dpi{120} cosseno= \frac{cateto\: adjacente}{hipotenusa}$

Em que a hipotenusa é sempre igual a $\dpi{120} l$ e os catetos variam de acordo com o ângulo.

Seno e cosseno de 30°:

Em relação ao ângulo de 30°, temos:

hipotenusa $\dpi{120} = l$
cateto oposto $\dpi{120} =\frac{l}{2}$
cateto adjacente $\dpi{120} =h = \frac{l\sqrt{3}}{2}$

Então:

$\dpi{120} seno \: 30^{\circ} = \frac{\frac{l}{2}}{l}=\frac{l}{2}\cdot \frac{1}{l} = \frac{1}{2}$

$\dpi{120} cosseno \: 30^{\circ} = \frac{\frac{l\sqrt{3}}{2}}{l} = \frac{l\sqrt{3}}{2}\cdot \frac{1}{l} = \frac{\sqrt{3}}{2}$

Seno e cosseno de 60°:

Em relação ao ângulo de 60°, temos:

hipotenusa $\dpi{120} = l$
cateto oposto $\dpi{120} =h = \frac{l\sqrt{3}}{2}$
cateto adjacente $\dpi{120} =\frac{l}{2}$

Então:

$\dpi{120} seno \: 60^{\circ} = \frac{\frac{l\sqrt{3}}{2}}{l} = \frac{l\sqrt{3}}{2}\cdot \frac{1}{l} = \frac{\sqrt{3}}{2}$

$\dpi{120} cosseno \: 60^{\circ} = \frac{\frac{l}{2}}{l}=\frac{l}{2}\cdot \frac{1}{l} = \frac{1}{2}$

Para calcular a tangente de qualquer um dos ângulos, basta utilizar a relação: $\dpi{120} tangente \: \alpha = \frac{seno \: \alpha}{cosseno \: \alpha}$

Seno e cosseno de 45°

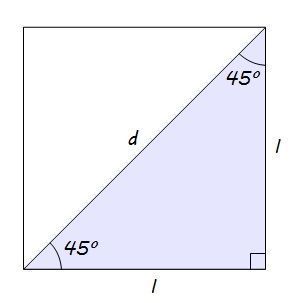
Para determinar seno e cosseno de 45°, vamos considerar um quadrado de lado l e traçar a diagonal d.

Como os quatro ângulos internos de um quadrado medem 90°, com a diagonal vamos obter o ângulo que desejamos, pois 90° : 2 = 45°.

Observe que a diagonal divide o quadrado em dois triângulos congruentes com ângulos internos iguais a 90°, 45° e 45° e lados $\dpi{120} l$ , $\dpi{120} l$ e $\dpi{120} d$ .