Perímetro do retângulo

O retângulo é um polígono que possui quatro lados, sendo classificado como quadrilátero.

O perímetro de um polígono é sempre calculado como a soma das medidas de todos os lados da figura. Assim, o perímetro do retângulo consiste na soma das medidas dos seus quatro lados.

Características do retângulo

O retângulo, além de ser classificado como quadrilátero, também é classificado como paralelogramo, por possuir os lados opostos paralelos.

Contudo, nem todo paralelogramo é um retângulo. Para ser retângulo, o paralelogramo deve possuir os quatro ângulos internos medindo 90°, ou seja, os quatro ângulos internos devem ser ângulos retos.

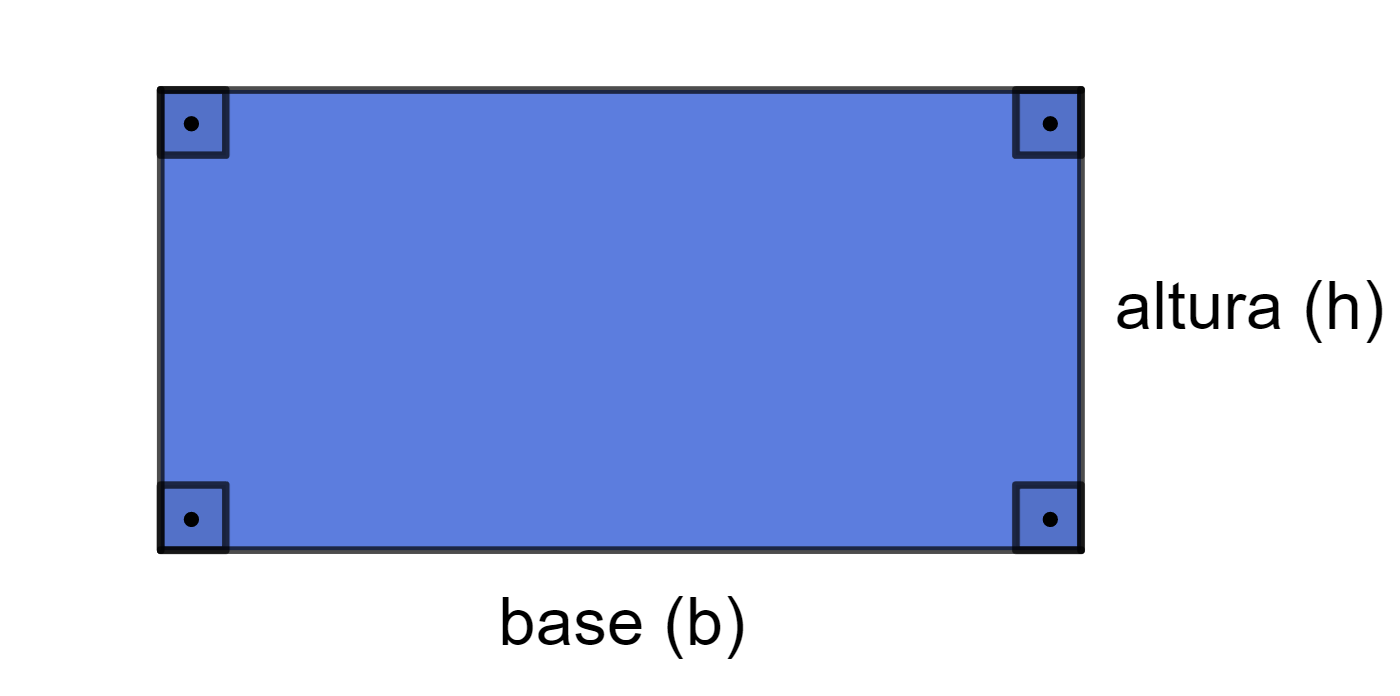
De modo geral, os retângulos são representados com dois lados maiores (base) e dois lados menores (altura), conforme é apresentado na figura a seguir:

Quando todos os lados do retângulo são de mesmo tamanho, tem-se um quadrado. Portanto, o quadrado é um caso particular de retângulo.

Perímetro do retângulo

O perímetro do retângulo é dado pela soma das medidas dos seus quatro lados. Como dois lados medem b (base) e dois lados medem h (altura), temos que:

P = b + b + h + h

⇒ P = 2b + 2h

⇒ P = 2 . (b + h)

Portanto, uma fórmula geral para o cálculo do perímetro de um retângulo é:

Em que:

• b: medida da base do retângulo;
• h: altura do retângulo.

Exemplo 1

Determine o perímetro de um retângulo cuja medida da base é 8 cm e altura é igual a 6 cm.

Temos b = 8 e h = 6.

Utilizando a fórmula do perímetro do retângulo, temos que:

P = 2 . (8 + 6)

⇒ P = 2 . 14

⇒ P = 28

Portanto, o perímetro do retângulo é igual a 28 cm.

Observação: O perímetro deve ser calculado com base e a altura na mesma unidade de medida.

Caso a base e a altura estejam em unidades diferentes, como uma em metros e a outra em centímetros, devemos fazer a transformação para que as duas estejam em metros ou as duas estejam em centímetros.

Exemplo 2

Determine o perímetro de um retângulo cuja medida da base é 12 m e altura é igual a 900 cm.

Primeiro, vamos converter a medida da altura para metros. Como 100 cm = 1 m, então, 900 cm = 9 m.

Agora, já podemos calcular o perímetro a partir da fórmula. Temos b = 12 e h = 9.

P = 2 . (12 + 9)

⇒ P = 2 . 21

⇒ P = 42

Portanto, o perímetro do retângulo é igual a 42 m.

Exemplo 3

Uma quadra de basquete tem 28 m de comprimento e 15 m de largura. Se um treinador deseja contornar a quadra com uma fita adesiva, quantos metros de fita são necessários?

A quadra de basquete tem o formato de um retângulo com b = 28 e h = 15, e a medida da fita necessária é igual à medida do seu contorno.

O contorno é o próprio perímetro. Então, vamos aplicar a fórmula do perímetro:

P = 2 . (28 + 15)

⇒ P = 2 . 43

⇒ P = 86

Portanto, são necessários 86 metros de fita adesiva para contornar a quadra de basquete.

Área do retângulo

Enquanto o perímetro do retângulo indica a medida do seu contorno, a área indica a medida da sua superfície e pode ser calculada multiplicando-se a medida da base pela altura.

Assim, a fórmula da área do retângulo é:

A = b . h

Em que:

• b: medida da base do retângulo;
• h: altura do retângulo.

Devemos ficar atentos à unidade de medida da área, que, ao contrário do perímetro, deve ser sempre elevada ao quadrado (cm², m², etc.).

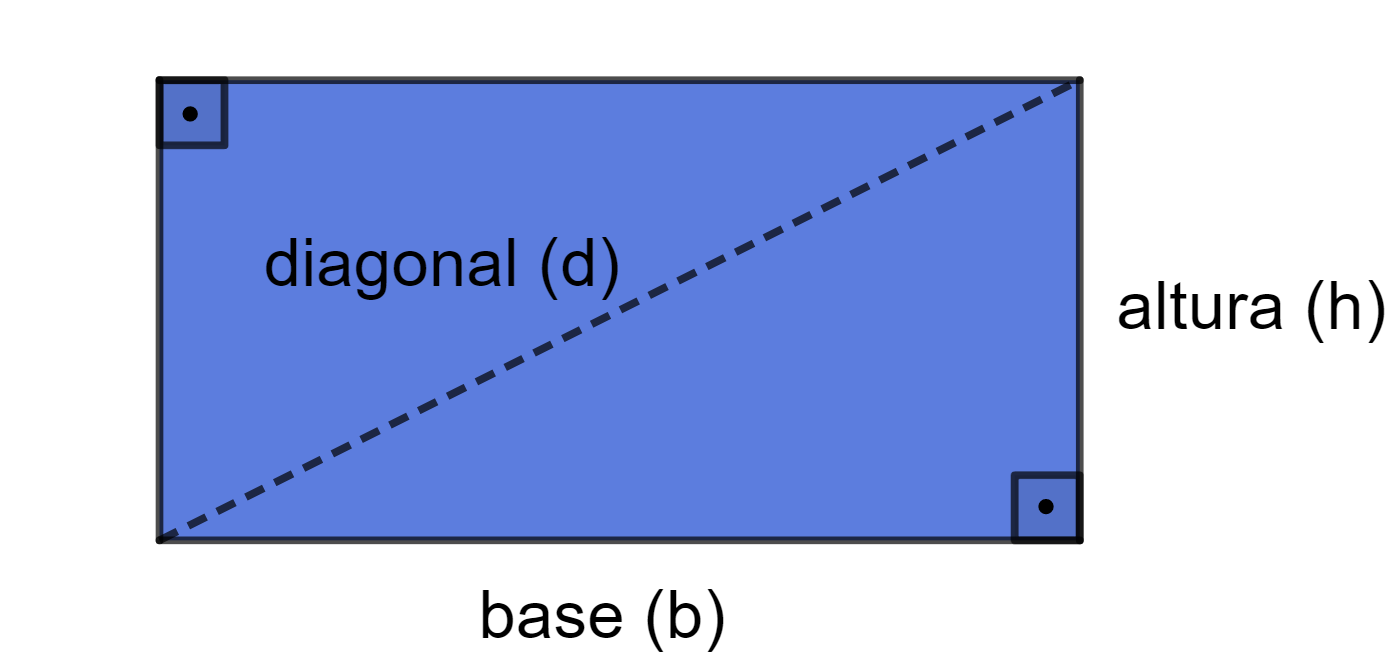
Diagonal do retângulo

As diagonais do retângulo são os segmentos de reta que ligam dois vértices não consecutivos e a medida desses segmentos pode ser calculada a partir da medida da base e da altura do retângulo.

Observe que, traçando a diagonal do retângulo, obtemos um triângulo retângulo. Portanto, a medida da diagonal (d), pode ser determinada pelo Teorema de Pitágoras.

A fórmula da diagonal do retângulo é:

Em que:

• b: medida da base do retângulo;
• h: altura do retângulo.

Você também pode se interessar:

• Perímetro do quadrado
• Perímetro do triângulo
• Perímetro do círculo
• Área e perímetro