Plano de aula – Bissetriz e mediatriz – 8º ano do Ensino Fundamental

Bissetriz e mediatriz são conceitos importantes na resolução de muitos problemas envolvendo figuras geométricas.

Contudo, devido às particulares de cada conceito e às similaridades existentes entre os dois, os alunos costumam se confundir e não entendem o significado de cada um nas figuras.

Assim, a construção da bissetriz e da mediatriz se torna fundamental para uma melhor compreensão das definições e da distinção entre elas.

Para lhe ajudar nessa tarefa, preparamos um plano de aula sobre esse tema, em conformidade com a habilidade EF08MA15 da Base Nacional Comum Curricular (BNCC).

Veja, a seguir, um plano de aula sobre bissetriz e mediatriz para o 8° ano do Ensino Fundamental.

Plano de aula – Bissetriz e mediatriz

TEMA: Bissetriz e mediatriz

HABILIDADES DA BNCC: (EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares.

TEMPO SUGERIDO: 2 horas e 30 minutos (3 aulas de 50 minutos)

OBJETIVOS:

• Compreender e diferenciar os conceitos de bissetriz e mediatriz;
• Construir bissetriz de ângulos e mediatriz de segmentos;
• Construir bissetriz e mediatriz de triângulos.

MATERIAL NECESSÁRIO:

• Régua;
• Transferidor;
• Compasso;
• Papel A4;
• Tesoura;
• Cola;
• Quadro e giz ou pincel.

DESENVOLVIMENTO:

Para esta aula, é necessário que os alunos já tenham conhecimento sobre ângulos, medidas de ângulos, tipos de ângulos e triângulos.

1º momento

Inicie a aula mostrando aos alunos como construir a bissetriz de um ângulo e mediatriz de um segmento com o transferidor.

Peça para construírem ângulos de 90°, 60°, 45° e 30° e traçarem a bissetriz. Em seguida, peça para construírem a mediatriz de segmentos de tamanhos diferentes.

Quando os alunos já estiverem familiarizados com a bissetriz e a mediatriz, ensine-os a construí-las com compasso e régua.

Essa construção exige alguns passos a mais, por isso, peça para que anotem, no caderno, o passo a passo da construção de cada uma.

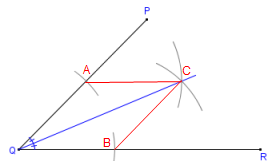
Passo a passo para a construção da bissetriz com compasso

1º) Com o transferidor, construa o ângulo desejado.

2º) Posicione a ponta seca do compasso no vértice do ângulo e trace um arco sobre cada um dos segmentos de reta que formam o ângulo.

3º) Marque os pontos de cruzamento entre os arcos e os segmentos do ângulo.

4º) Sem mexer na abertura do compasso, posicione a ponta seca em cada um desses pontos e trace outros dois arcos.

5º) Marque o ponto de intersecção entre esses dois arcos traçados.

6º) Trace um segmento de reta que liga o vértice a esse ponto de intersecção.

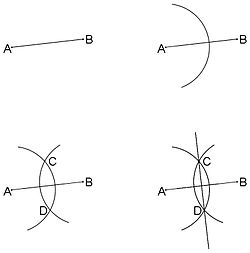
Passo a passo para a construção da mediatriz com compasso

1º) Com a régua, faça um segmento de reta.

2º) Abra o seu compasso de modo que a abertura seja um pouco maior que a metade do segmento de reta que você traçou.

3º) Posicione a ponta seca do compasso em uma das extremidades do segmento e faça a metade de um círculo sobre o próprio segmento.

4º) Posicione a ponta seca do compasso na outra extremidade e faça outra metade de um círculo sobre o segmento;

5º) Marque os dois pontos onde os semicírculos se encontram e trace uma reta que passa por eles.

2º momento

Agora, a ideia é que os alunos construam a bissetriz dos ângulos de um triângulo, e a mediatriz de cada lado de um triângulo, utilizando dobraduras.

Distribua uma folha de papel A4 para cada aluno, peça que desenhem dois triângulos iguais e recortem.

Instruções para o 1º triângulo

1º) Fazendo dobraduras, obtenha as três bissetrizes do triângulo.

2º) Marque o ponto de encontro entre essas três bissetrizes (incentro).

3º) Cole o triângulo no caderno.

4º) Posicione a ponta seca do compasso no incentro, abra-o até o ponto mais próximo de um dos lados e trace uma circunferência.

Peça que respondam no caderno: A circunferência passa pelos três vértices do triângulo?

Instruções para o 2º triângulo

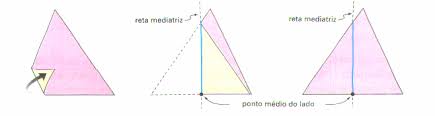
1º) Fazendo dobraduras, obtenha as três mediatrizes do triângulo.

2º) Marque o ponto de encontro entre essas três bissetrizes (circuncentro).

3º) Cole o triângulo no caderno.

4º) Posicione a ponta seca do compasso no circuncentro, abra-o até um dos vértices e trace uma circunferência.

Peça que respondam no caderno: A circunferência passa pelos três vértices do triângulo?

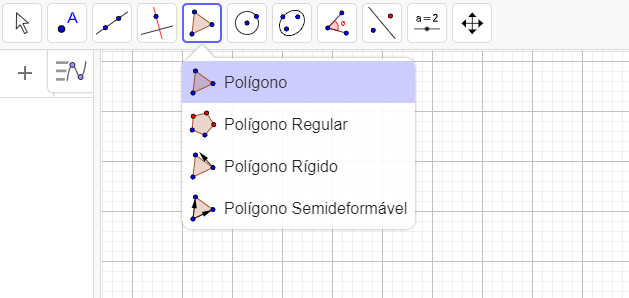
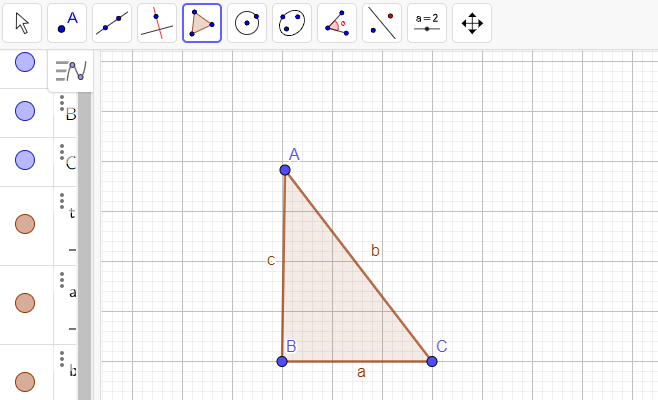
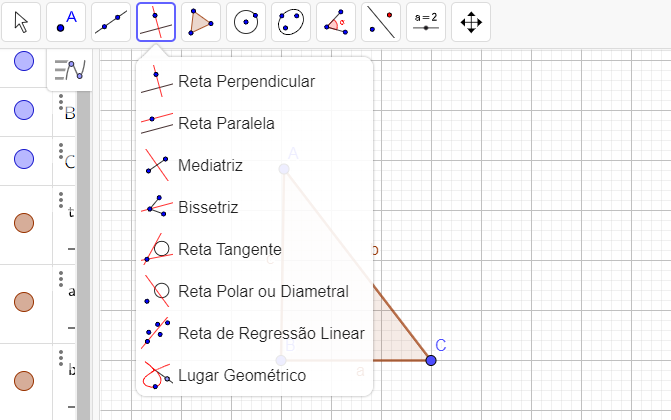
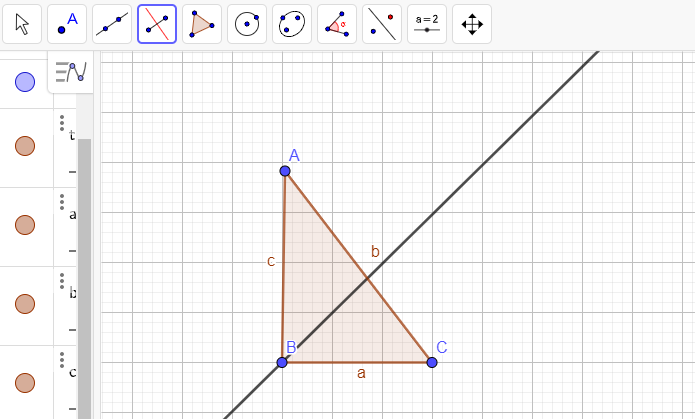
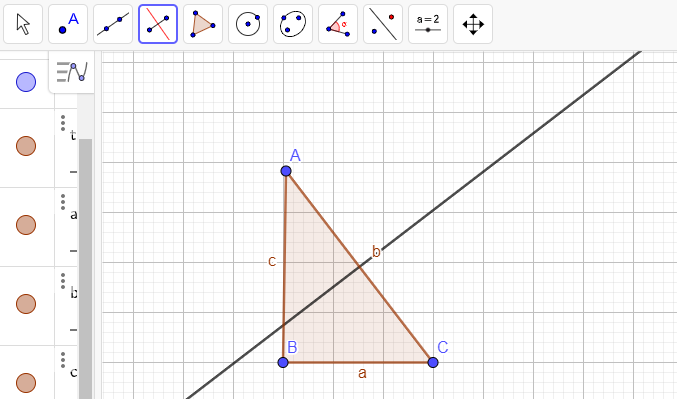
Se houver disponibilidade de computadores para os alunos, sugerimos que complemente suas aulas sobre construção de mediatriz e bissetriz com o uso do software Geogebra.

O Geogebra é gratuito e pode ser utilizado no próprio computador, através do download no site. Também há a opção de utilizar o programa online nesse mesmo site.

AVALIAÇÃO:

A avaliação poderá ser feita a partir da observação do desempenho dos alunos durante as aulas. Além disso, faça perguntas como:

• O que vocês acharam de construir a bissetriz e a mediatriz?
• Qual forma de construir vocês mais gostaram?
• O que diferencia a bissetriz da mediatriz em um triângulo?

Para baixar esse plano em PDF, clique aqui!

Você também pode se interessar:

• Semelhança de triângulos
• Congruência de formas geométricas
• Ângulos colaterais internos e externos
• Plano de aula – Polígonos regulares – 8º ano do Ensino Fundamental