Setor da região circular – Como calcular a área

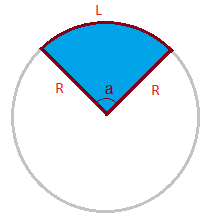
O setor circular é uma região do círculo que parte do centro e é limitada por dois segmentos de reta correspondentes ao raio R.

O ângulo a na figura é chamado de ângulo central do setor circular.

Pelo formato, o setor circular pode ser visto como uma fatia de pizza.

Área do setor circular

Em um círculo, o ângulo central corresponde 360° ou 2π em radianos e área do círculo de raio R é dada por πR².

Como o setor circular é uma parte do círculo, sua área pode ser determinada a partir de uma regra de três simples com base nas medidas do círculo, sendo proporcional ao seu ângulo central a.

Veja:

	Ângulo central	Área
Círculo	360°	πR²
Setor circular	a	A

Portanto, temos a seguinte proporção:

Conhecendo o ângulo central a, queremos descobrir a área A do setor circular. Pela propriedade fundamental das proporções (multiplicação cruzada), temos que:

Portanto, a fórmula da área do setor circular é dada por:

Em radianos, a fórmula equivalente é:

Já que 360° = 2π.

Exemplo:

Calcule a área de um setor circular de ângulo central igual a 45° de um círculo de raio igual a 8 cm.

Temos a = 45° e R = 8. Considerando π ≅ 3,14 e aplicando esses valores na fórmula, temos que:

Portanto, a área do setor circular é igual a 25,12 cm².

Você também pode se interessar:

• Arcos e movimento circular
• Arcos com mais de uma volta
• Perímetro do círculo
• Comprimento do círculo
• Fórmulas de adição e subtração de arcos