Trigonometria em um triângulo qualquer
Aprenda as leis de trigonometria que relacionam os ângulos e lados de qualquer triângulo, seja ele retângulo ou não.
Embora a trigonometria seja comumente associada ao estudo do triângulo retângulo, envolvendo hipotenusa e catetos oposto e adjacente, a trigonometria é uma parte da matemática que se encarrega das relações entre lados e ângulos de triângulos em geral.
Relembre os tipos de triângulos:
- Triângulo retângulo: é o triângulo que possui um ângulo de 90°;
- Triângulo acutângulo: é o triângulo que possui os três ângulos menores que 90°;
- Triângulo obtusângulo: é o triângulo que possui um ângulo maior que 90°.
No triângulo retângulo, utiliza-se as relações trigonométricas. Já as leis que vamos ver a seguir, lei dos senos e cossenos, ainda que possam ser utilizadas em qualquer triângulo, são mais usadas nos triângulos acutângulos e obtusângulos.
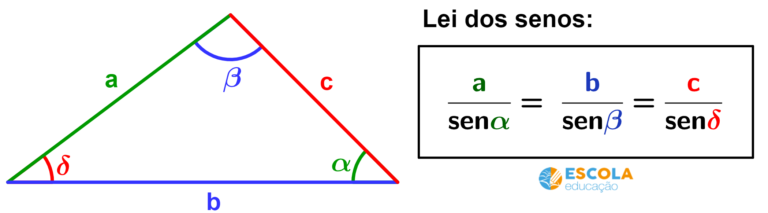
Lei dos senos
A lei dos senos diz que, em um triângulo qualquer, os quocientes entre as medidas dos lados e os senos dos ângulos opostos são iguais.
Exemplo: Em um triângulo com ,
e b = 20 cm, determine a medida do terceiro ângulo e dos outros lados.
Em qualquer triângulo, a soma dos ângulos internos é sempre igual a 180°, ou seja:
Então:
Pela lei dos senos, temos a seguinte relação:
Considerando a primeira igualdade, podemos determinar o valor do lado a:
Multiplicamos cruzado:
Os valores do seno e cosseno podem ser obtidos através de uma calculadora ou de uma tabela trigonométrica.
Agora, considerando a segunda igualdade, podemos determinar o valor do lado c:
Multiplicamos cruzado:
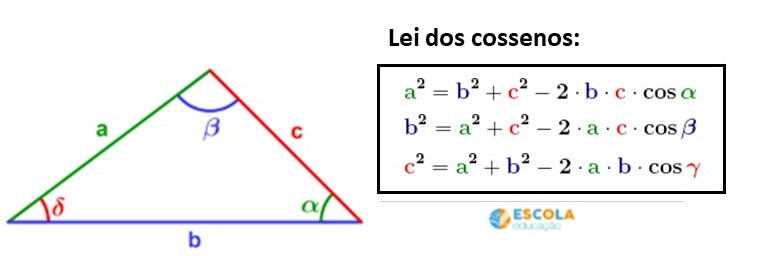
Lei dos cossenos
A lei dos cossenos é composta de três equações que relacionam o quadrado de cada lado aos outros dois lados e ao cosseno do ângulo oposto ao lado.
A partir da lei dos cossenos, podemos determinar as medidas desconhecidas quando sabemos os valores dos três lados ou quando sabemos dois lados e um ângulo compreendido entre eles.
Exemplo: Em um triângulo com lados a = 18, b = 25 e c = 30, determine a medida do ângulo .
Vamos utilizar a primeira equação da lei dos cossenos para encontrar o ângulo :
Você também pode se interessar:
- Lista de exercícios sobre lei dos senos
- Lista de exercícios de trigonometria
- Seno e cosseno de ângulos obtusos


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.