Lista de exercícios de matrizes
Confira uma lista de exercícios resolvidos sobre matrizes. Os exercícios envolvem operações entre matrizes, transposta, determinante, e muito mais!
As matrizes podem ser classificadas em diferentes tipos e entre elas podem ser realizadas várias operações algébricas. Por isso, esse é um assunto que costuma causar dor de cabeça nos alunos do ensino médio.
O segredo para se dar bem com as matrizes é conhecer bem as definições e praticar, resolvendo muitos exercícios. Pensando nisso, preparamos uma lista de exercícios resolvidos sobre matrizes. Confira!
Lista de exercícios de matrizes
Questão 1. Dadas as matrizes A e B abaixo, calcule 2A – B.
Questão 2. Construa uma matriz A de ordem 2 x 3 formada por elementos do tipo:
Questão 3. Considerando a matriz B, encontre a matriz transposta e calcule .
Questão 4. Determine os valores de a e b , sabendo que:
Questão 5. Determine os valores de a e b , sabendo que:
Questão 6. Considerando as matrizes A e B, calcule o produto A . B.
Questão 7. Calcule o determinante das matrizes C e D, abaixo:
Questão 8. Calcule o determinante da matriz M, abaixo:
Resolução da questão 1
Para saber como fazer operações entre matrizes, veja: adição e subtração de matrizes.
Resolução da questão 2
A matriz A tem 2 linhas e 3 colunas, ou seja:
Sabendo que cada elemento é do tipo:
Vamos calcular cada elemento e depois substituir os valores na matriz A:
Resolução da questão 3
Resolução da questão 4
Temos que:
Ou seja,
a – 1 = 7 ⇒ a = 7 + 1 ⇒ a = 8
2b = 22 ⇒ b = 22/2 ⇒ b = 11
Resolução da questão 5
Temos que:
Assim,
a + b = 4 e a – b = 2
Precisamos encontrar a e b que satisfaçam essas duas equações ao mesmo tempo. Então, temos que resolver um sistema de equações.
De a + b = 4, temos que:
a = 4 – b
Substituindo a por 4 – b outra equação:
a – b = 2
4 – b – b = 2
4 – 2b = 2
-2b = 2 – 4
-2b = -2
b = 2/2
b = 1
Agora, determinamos o valor de a:
a = 4 – b
a = 4 – 1
a = 3
Portanto, temos a = 3 e b = 1.
Resolução da questão 6
Para saber mais, veja: multiplicação de matrizes.
Resolução da questão 7
Para calcular o determinante de uma matriz de ordem 2, basta multiplicar os elementos da diagonal principal e subtrair pelo produto dos elementos da diagonal secundária.
|C| = -2 . 1 – 3.6 = -2 – 18 = – 20
|D| = 3 . 0 – (-8) . 4 = 0 – (-32) = 32
Resolução da questão 8
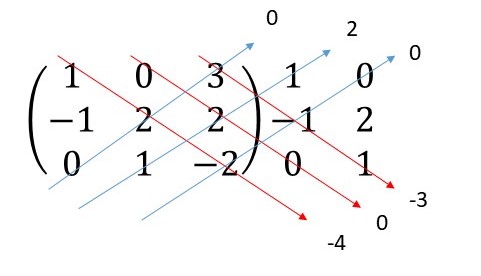
Para calcular o determinante de uma matriz de ordem 3, devemos escrever as duas primeiras colunas a direita da matriz. Depois, calcular o produto de cada diagonal principal e de cada diagonal secundária.
Por fim, somamos os produtos das diagonais principais e subtraímos os produtos das diagonais secundárias.
|M| = 0 + 2 + 0 – (-3 + 0 -4) = 2 – (-7) = 9
Para saber mais, veja: determinante de uma matriz.
Você também pode se interessar:
- Escalonamento de matrizes – Resolver sistemas lineares
- Lista de exercícios de regra de três
- Lista de exercícios de potenciação
- Lista de exercícios de área de figuras planas

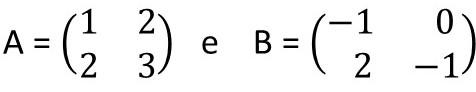
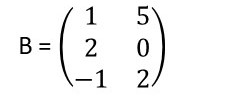
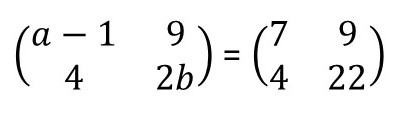
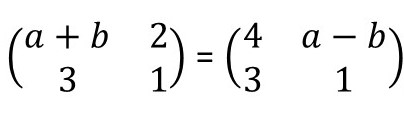
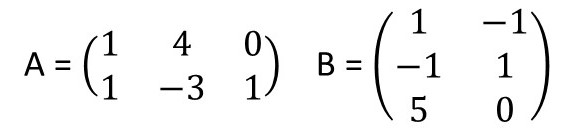
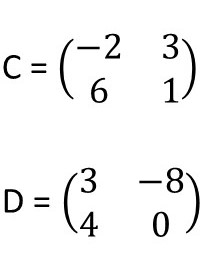
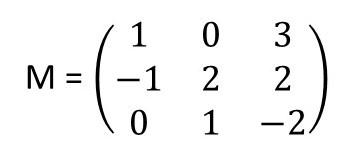
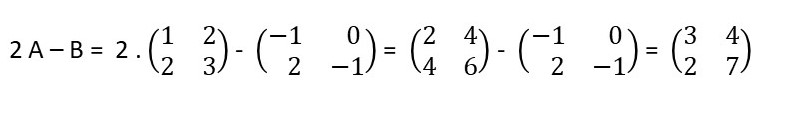
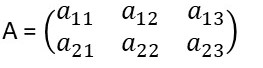
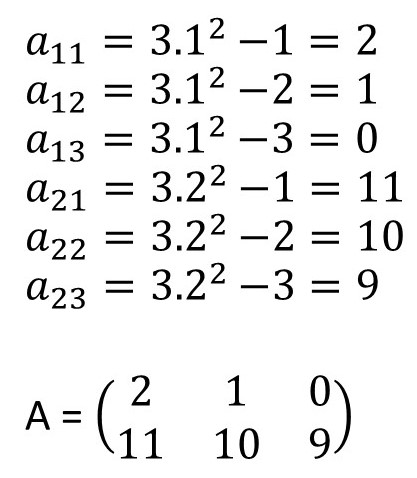
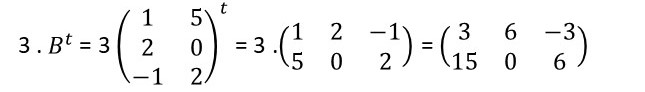
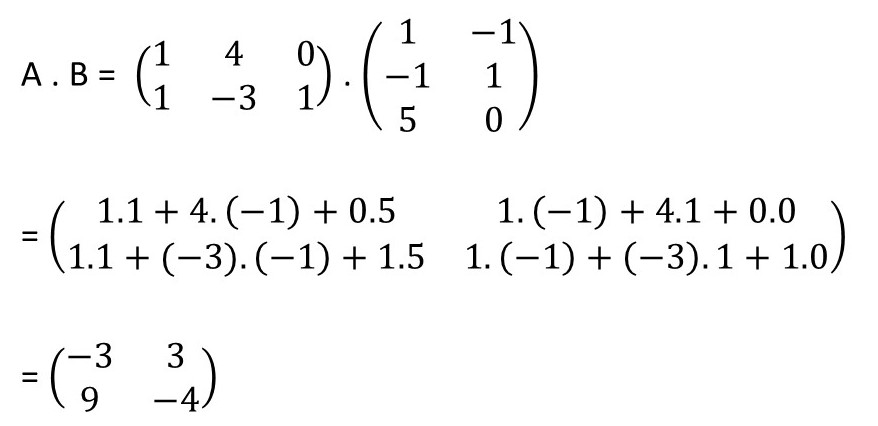
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.