Plano de aula – Relações de proporcionalidade em situações cotidianas – 9º ano do Ensino Fundamental
Confira um plano de aula sobre relações de proporcionalidade para o 9º ano, de acordo com a habilidade EF09MA14 da Base Nacional Comum Curricular (BNCC).
Há mais de 2000 anos, os matemáticos já compreendiam a importância das relações de proporcionalidade e suas aplicações em problemas reais.
Tales de Mileto, o famoso filósofo e matemático que viveu aproximadamente entre os anos 624 e 548 a.C., teria calculado a altura de uma enorme pirâmide utilizando apenas seus conhecimentos de proporcionalidade em triângulos.
Contudo, nos dias atuais, não só a geometria, mas a matemática em geral ainda é vista pelos estudantes como algo distante da realidade, como uma ciência repleta de fórmulas, conceitos e definições abstratas e sem utilidade.
Assim, é notável a necessidade que há em fazer a conexão entre a teoria e o mundo real, a partir da abordagem de problemas práticos em situações cotidianas.
Confira a seguir, um plano de aula sobre relações de proporcionalidade em situações cotidianas para o 9º ano do ensino fundamental, em conformidade coma habilidade EF09MA14 da Base Nacional Comum Curricular (BNCC).
Plano de aula – Relações de proporcionalidade em situações cotidianas
TEMA: Proporcionalidade
HABILIDADES DA BNCC: (EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
TEMPO SUGERIDO: 2 horas e 30 minutos (3 aulas de 50 minutos)
OBJETIVOS:
- Aplicar as relações de proporcionalidade em problemas que ilustram situações reais, como cálculo de alturas e longitudes de segmentos.
MATERIAL NECESSÁRIO:
- Quadro ou lousa;
- Giz ou pincel.
DESENVOLVIMENTO:
1º momento
O objetivo principal da aula é resolver problemas envolvendo proporcionalidade. Para isso, inicie a aula relembrando alguns conteúdos necessários, como razão e proporção, semelhança de triângulos e teorema de Tales.
Em seguida, proponha um problema que envolva o uso de relações de proporcionalidade. Resolva esse problema junto com eles, dando tempo para pensarem, discutirem ideias e traçarem uma forma de solucioná-lo.
Resolução:
Os triângulos formados são triângulos retângulos, pois, em cada caso, o segmento de reta correspondente à altura forma, com o solo, um ângulo reto.
Além disso, em um mesmo horário, os raios solares são paralelos, assim, os outros dois ângulos correspondentes dos triângulos também têm a mesma medida, são congruentes.
Logo, pelo caso de semelhança AA, os triângulos são semelhantes.
Pela semelhança, temos que:
Multiplicando cruzado:
Portanto, a altura do prédio é 29,16 m.
2º momento
Agora, é o momento dos alunos trabalharem em grupos.
Prepare vários problemas envolvendo situações cotidianas para que os alunos resolvam a partir das relações de proporcionalidade.
Divida a turma em grupos não muitos grandes (em torno de 4 ou 5 alunos cada). Distribua um problema para cada grupo e estabeleça um tempo de até 20 minutos para que eles o resolvam em conjunto.
Após esse tempo, cada grupo deverá escolher um representante para ir à frente explicar o problema e apresentar a solução.
Sugestões de problemas:
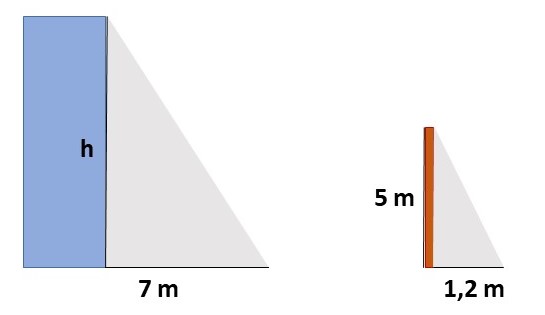
Resposta esperada: 8,01 m.
Resposta esperada: 6,91 m.
Resposta esperada: 2,4 m; 1,52 m e 1,28 m.
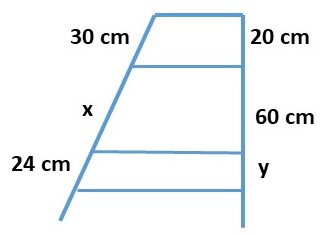
Resposta esperada: x = 90 cm e y = 16 cm.
AVALIAÇÃO:
A avaliação poderá ser feita a partir da observação dos alunos durante a aula.
Analise a participação nas atividades e a forma como eles trabalham em grupo para solucionar o problema proposto.
Observe se eles compreendem a importância das relações de proporcionalidade em situações cotidianas e conseguem utilizá-las de forma adequada em cada situação.
Para baixar o plano sobre relações de proporcionalidade em PDF, clique aqui!
Você também pode se interessar:
- Lista de exercícios sobre semelhança de triângulos
- Lista de exercícios sobre teorema de Tales
- Plano de aula de Matemática – Teorema de Pitágoras
- Plano de aula – Proporcionalidade dos triângulos – 9º ano do Ensino Fundamental
- Plano de aula – Teorema de Tales – 9º ano do Ensino Fundamental

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.