Sequência de Fibonacci
Conheça a sequência matemática considerada "divina" ou da "perfeição", por ser observada em quase tudo o que há de mais belo e agradável aos olhos!
A sequência de Fibonacci, também conhecida como sequência divina, é chamada assim por ser observada em quase tudo o que há de mais belo na natureza e por ter aplicações em diversas áreas, como música, poesia, arquitetura, entre outras.
Formada apenas por números inteiros, a sequência de Fibonacci é infinita. Veja os primeiros números:
Considera-se que o primeiro registro da sequência tenha sido no livro Liber Abaci (1202) do matemático italiano Leonardo Pisa, também conhecido por Fibonacci, o que levou ao nome da sequência.
Coelhos de Fibonacci
Um dos problemas clássicos que envolvem a sequência de Fibonacci e sua origem é o do crescimento de uma população de coelhos.
Com algumas suposições, Fibonacci verificou que, ao longo de meses, os coelhos se reproduziam da seguinte forma:
- 1° mês: inicia-se com 1 casal de coelhos.
- 2° mês: continua-se com 1 casal de coelhos, pois eles ainda não se desenvolveram o suficiente para reproduzir.
- 3° mês: os coelhos se reproduzem e tem-se, então, 2 casais de coelhos.
- 4° mês: o primeiro casal se reproduz novamente, mas o segundo casal ainda não se reproduz. Fica-se com 3 casais de coelhos.
- 5° mês: o primeiro casal se reproduz, o segundo casal se reproduz, mas o terceiro casal ainda não. Fica-se, agora, com 5 casais de coelhos.
- 6° mês: o primeiro, o segundo e o terceiro casal se reproduz, mas o quarto e o quinto casal ainda não. Totaliza-se, nesse mês, 8 casais de coelhos.
E assim por diante, ao longo do tempo.
Com isso, Fibonacci observou que o número de casais em um mês era sempre igual à soma do número de casais dos dois meses anteriores, formando uma sequência: 1, 1, 2, 3, 5, 8, 13, …
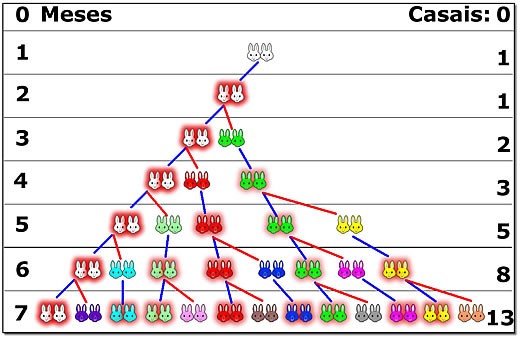
Veja que, para saber o número de casais do 7º mês, basta somar as quantidades do 6º e 5º mês: 8 + 5 = 13.
Qualquer que seja o mês, para saber o total de coelhos, só é necessário conhecer as quantidades dos dois meses anteriores.
Fórmula da sequência de Fibonacci
Toda sequência possui uma regra que define como ela é formada, ou seja, os números da sequência não são aleatórios, há um motivo de cada um estar lá.
A sequência de Fibonacci começa pelo número 1, em seguida, vem ele mesmo, e os próximos números são obtidos pela seguinte fórmula:
Exemplos:
Se queremos saber o 3º número da sequência, basta somar o 2º e o 1º número da sequência:
Se queremos saber o 4º número da sequência, basta somar o 3º e o 2º número da sequência:
Se quisermos saber o 5º número da sequência, basta somar o 4º e o 3º número da sequência:
Número de ouro
O número 1,61803399 é chamado de número de ouro, número áureo ou proporção de Deus, pois representa a perfeição.
Esse número está relacionado com a sequência de Fibonacci. Observe que, se dividirmos qualquer número da sequência pelo número anterior, o resultado será sempre próximo de 1,61.
Exemplos: ,
,
.
Retângulo de ouro
O retângulo de ouro, ou retângulo dourado, é qualquer retângulo cuja medida da base dividida pela altura resulta no número de ouro.
Então, sempre que as medidas do retângulo são dois números consecutivos da sequência de Fibonacci, o retângulo é de ouro.
Exemplo: um retângulo de base 13 cm e altura 8 cm é um retângulo de ouro.
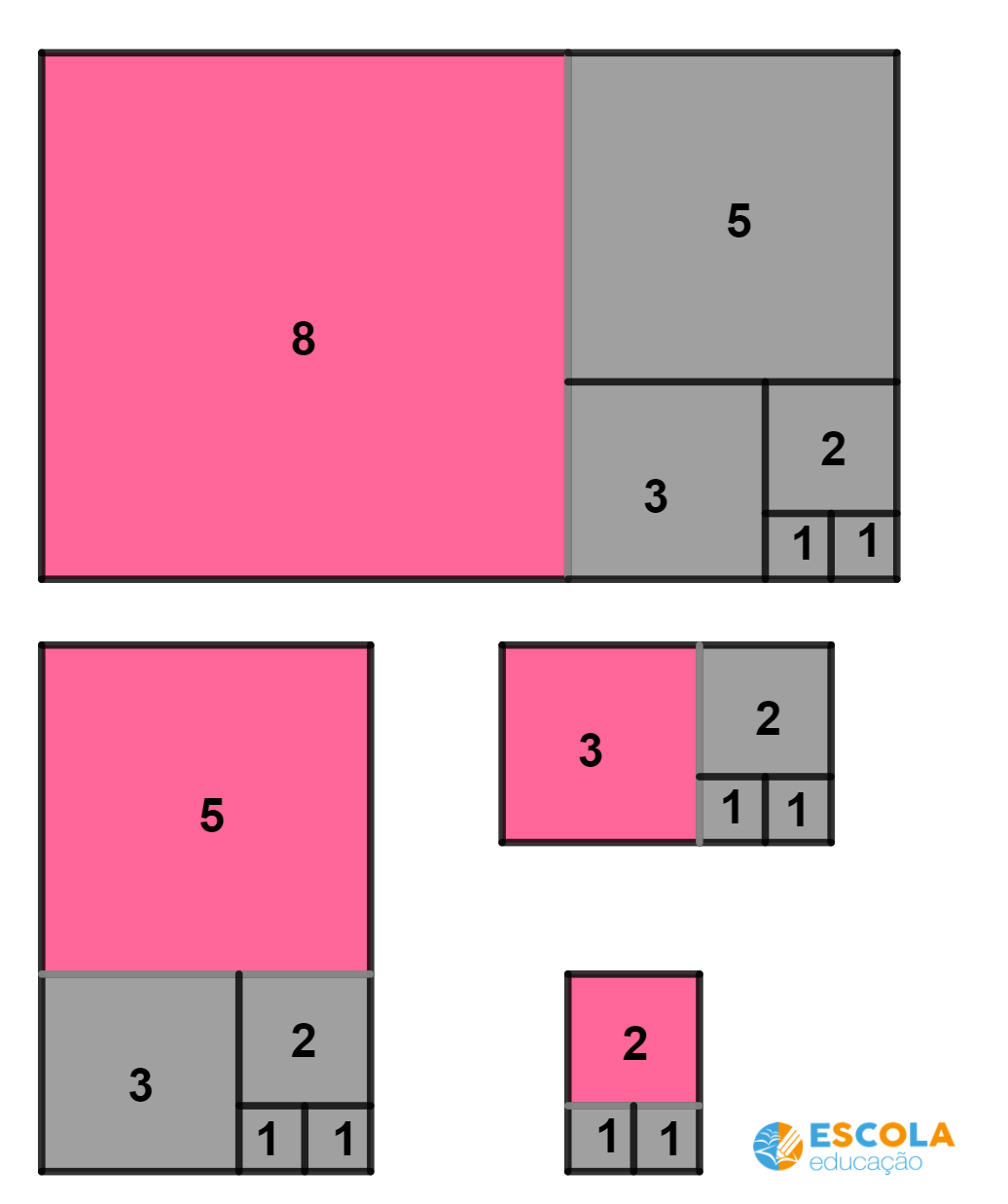
Uma característica importante dos retângulos de ouro é que eles são formados por outros retângulos de ouro menores.
Consequentemente, em retângulos de ouro, podemos observar a nossa belíssima sequência de Fibonacci.
Espiral de Fibonacci
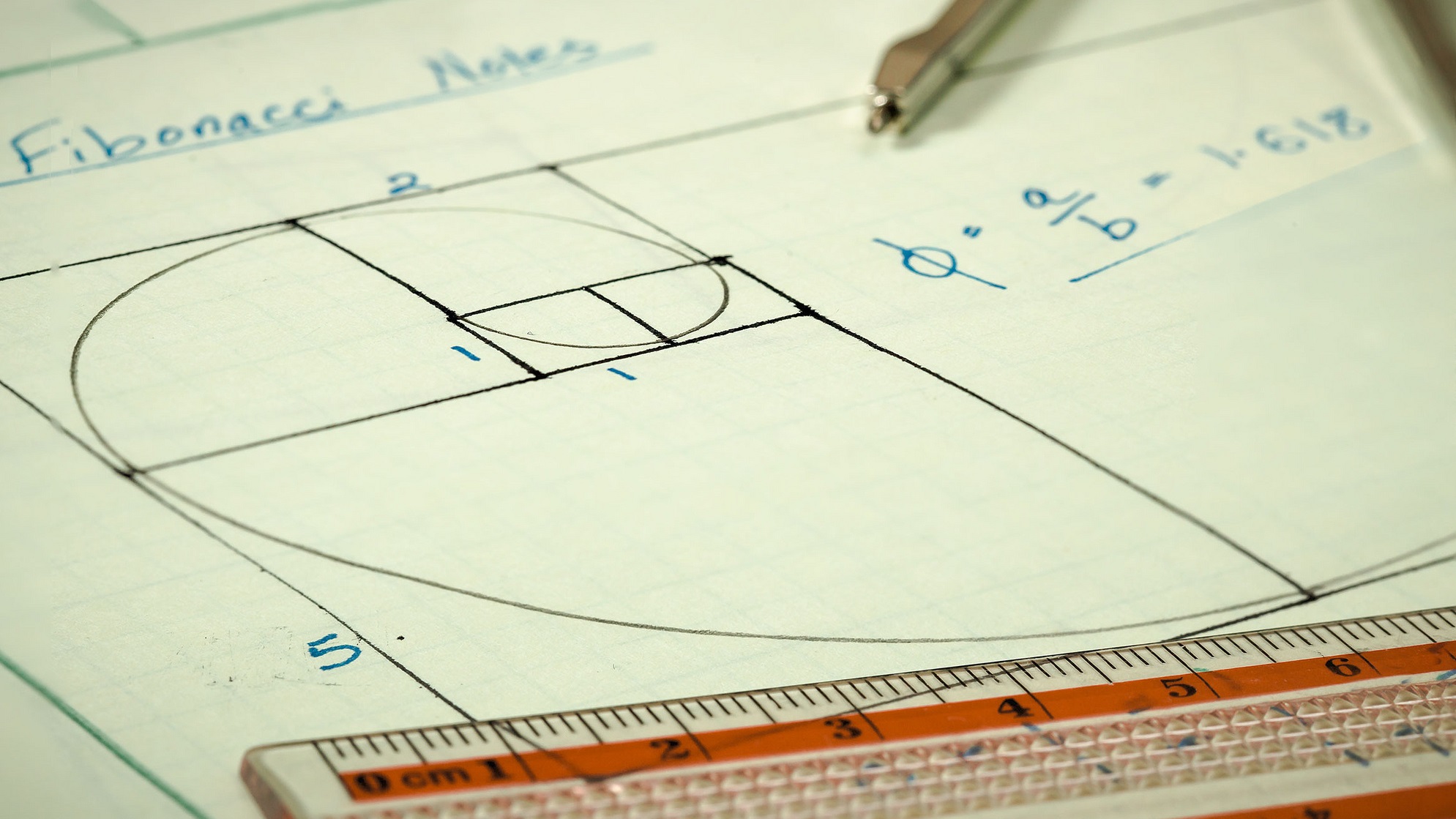
Traçando um arco no retângulo de ouro, obtém-se a chamada de Espiral de Fibonacci.
Essa espiral pode ser amplamente percebida na natureza, em construções, em obras de arte e muitas outras coisas que são harmoniosas aos nossos olhos, por trazerem consigo a proporção áurea.

Sequência de Fibonacci na poesia
Apesar da sequência ser referenciada ao matemático Fibonacci, alguns autores defendem que a sequência teria uma origem poética, tendo sido descrita quase dois séculos antes, por matemáticos indianos, em poemas de uma língua antiga da Índia, o sânscrito.
Contudo, não há um consenso sobre quem descobriu a sequência. Mas vamos entender como os números de Fibonacci estariam presentes nesse tipo de poesia.
No sânscrito, há sílabas curtas e largas e elas são medidas por unidades: 1 unidade, 2 unidades, e assim por diante.
Alguns poemas tinham o mesmo número de unidades por versos, mas para que isso acontecesse haviam algumas restrições em relação às sílabas serem curtas ou largas.
- Poemas com 1 unidade em cada verso deveriam ter apenas uma sílaba curta em cada verso.
- Poemas com 2 unidades em cada verso deveriam ter apenas uma sílaba larga ou duas sílabas curtas.
- Poemas com 3 unidades em cada verso deveria ter apenas uma sílaba larga e uma curta, ou uma curta e uma larga, ou três sílabas curtas seguidas.
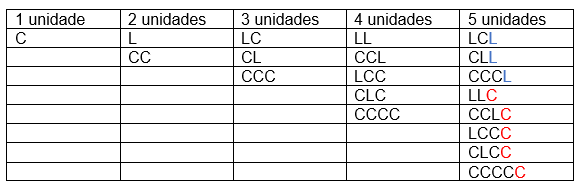
Denotando as sílabas curtas por C e as sílabas largas por L, podemos montar um quadro:
Então, para 1, 3, 3, 4, 5 unidades, o número de possibilidades é 1, 2, 3, 5, 8, que são os números da sequência de Fibonacci.
Além disso veja que, por exemplo, na coluna de 5 unidades, temos 3 possibilidades que terminam com letra L e 5 possibilidades que terminam com letra C, e 3 + 5 = 8.
Podemos concluir que, independente de quem a tenha descoberto, a sequência de Fibonacci é mesmo impressionante e suas aplicações estão além da matemática, na verdade, ela está presente em quase tudo o que existe!
Você também pode se interessar:
- Fractais
- Curiosidades sobre os números
- Curiosidades da matemática – Fatos matemáticos super interessantes
- Jogos de matemática usando calculadora

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.