Sinais de uma equação do 2° grau

Uma função do 2° grau é qualquer função da forma f(x) = ax² + bx + c = 0, com a, b e c sendo números reais e a diferente de zero.

Estudar os sinais de uma função do 2° grau significa dizer para quais valores de x a função é positiva, negativa ou igual a zero.

Desse modo, precisamos identificar quais são os valores de x onde temos:

f(x) > 0 → função positiva

f(x) < 0 → função negativa

f(x) = 0 → função nula

Mas como podemos saber isso? Uma das formas de estudar o sinal de uma função do 2° grau é por meio do seu gráfico, que é uma parábola.

Sinais de uma função do 2° grau a partir do gráfico

No plano cartesiano, f(x) > 0 corresponde a parte da parábola que está acima do eixo x, f(x) = 0 a parte da parábola que intercepta o eixo x e f(x) < 0, a parte da parábola que está abaixo do eixo x.

Então, só precisamos fazer um esboço da parábola para identificar os sinais da função. O esboço é feito simplesmente sabendo qual a concavidade da parábola e se ela intercepta ou não o eixo x, e se intercepta, em quais pontos isso acontece.

Podemos ter seis casos diferentes.

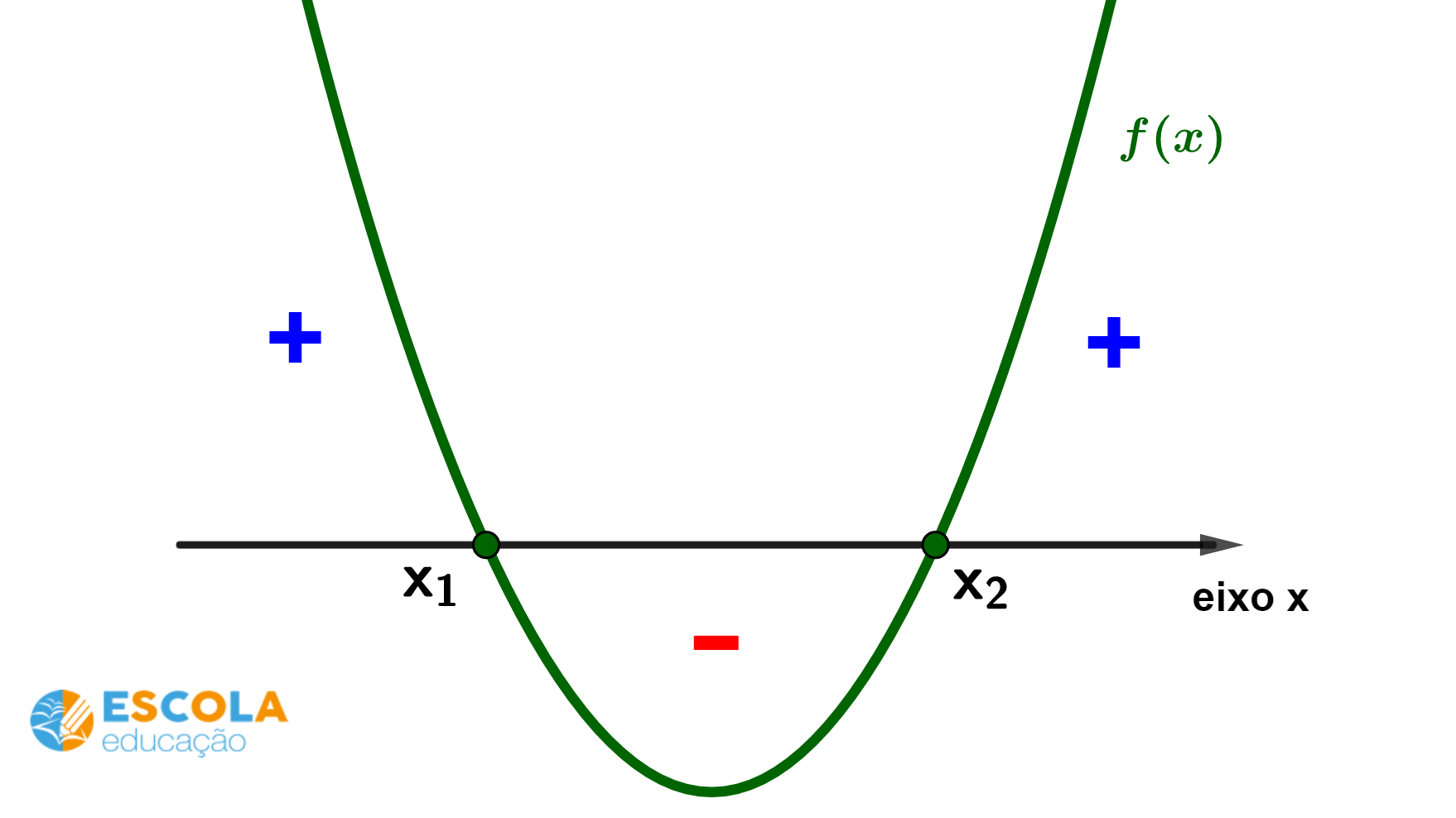
Caso 1) Sinais de uma função do 2° grau com duas raízes  e  distintas e concavidade da parábola voltada para cima.

A partir do gráfico, podemos identificar que:

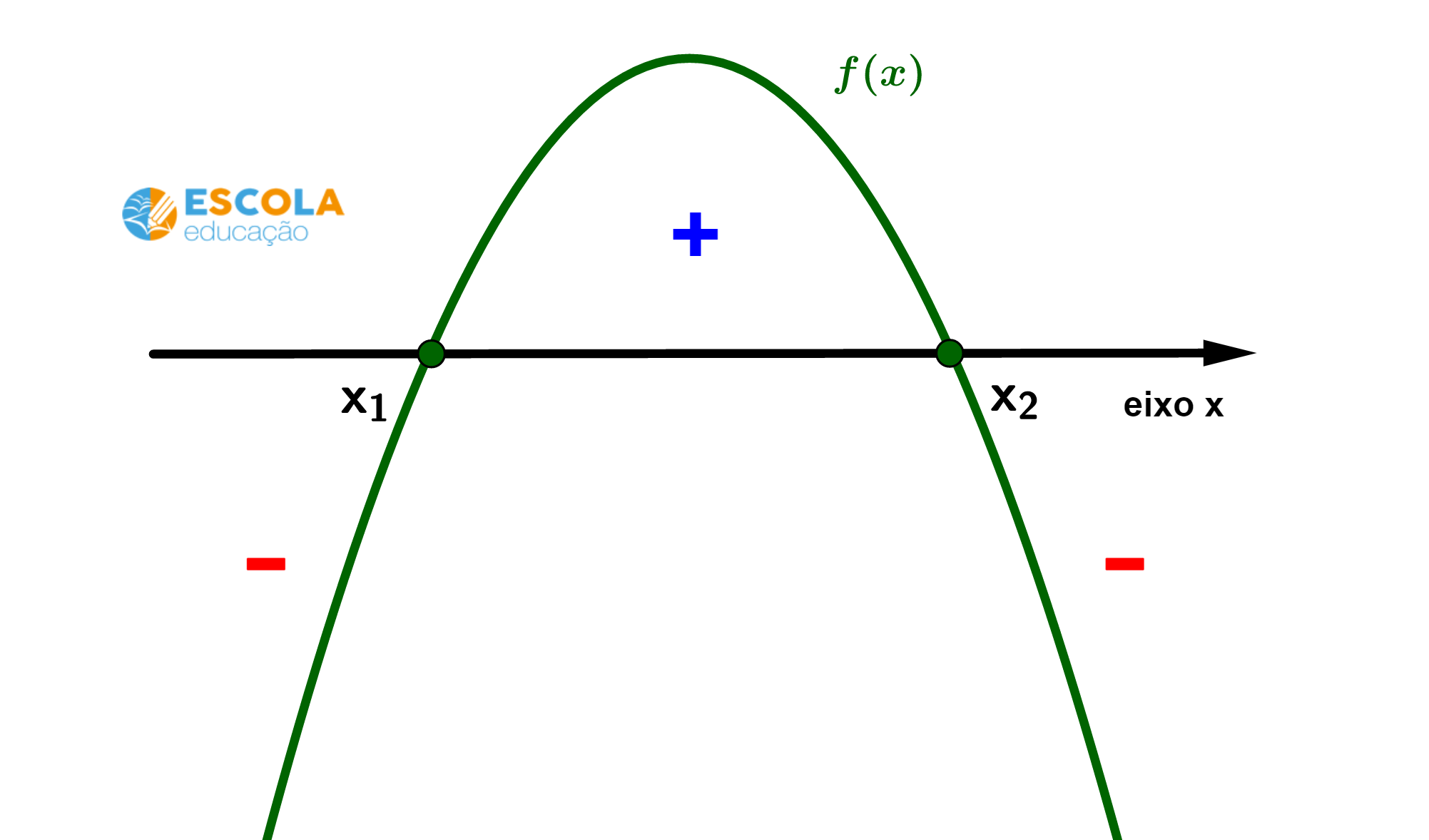
Caso 2) Sinais de uma função do 2° grau com duas raízes  e  distintas e concavidade da parábola voltada para baixo.

A partir do gráfico, podemos identificar que:

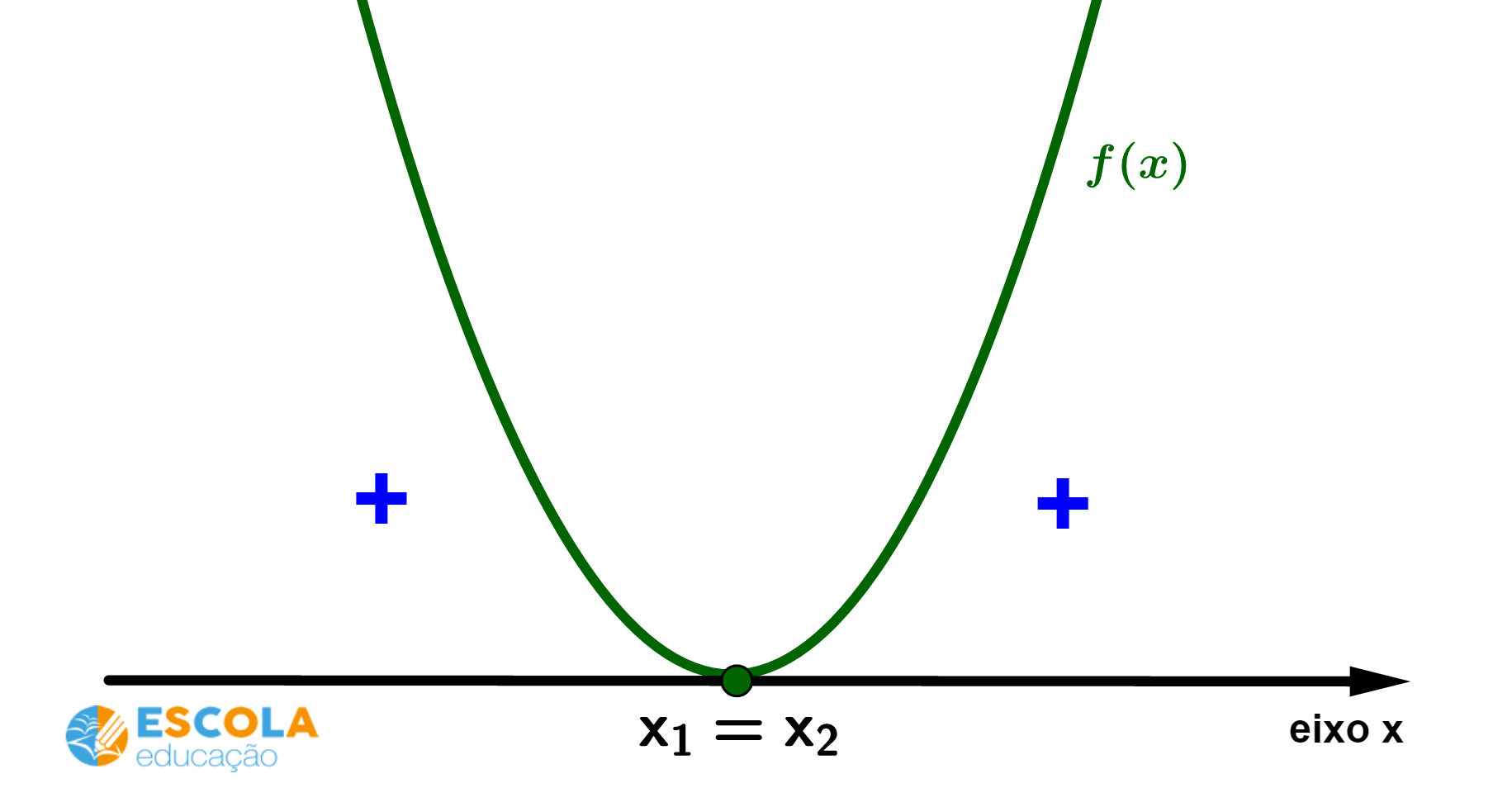
Caso 3) Sinais de uma função do 2° grau com duas raízes  e  iguais e concavidade da parábola voltada para cima.

A partir do gráfico, podemos identificar que:

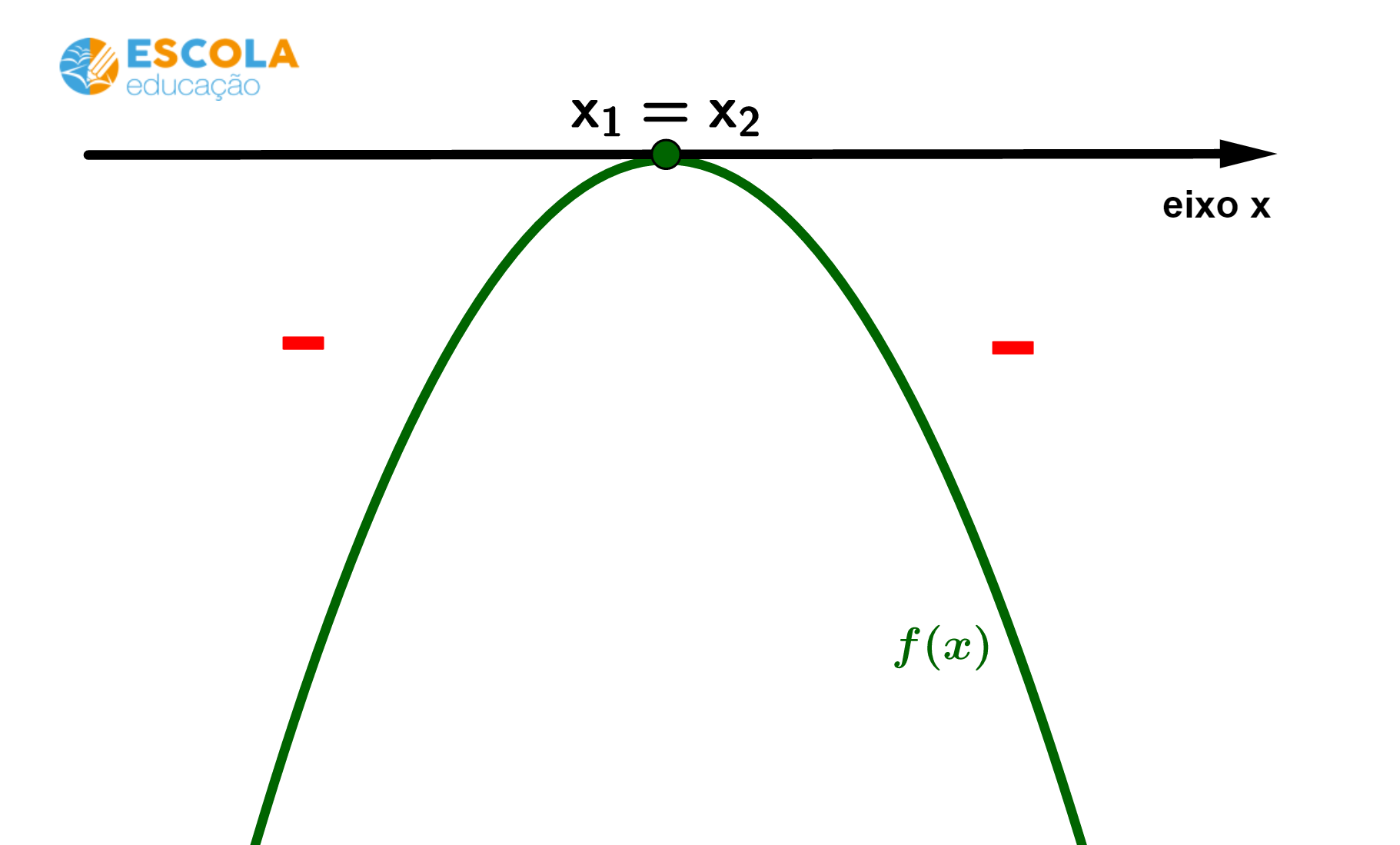
Caso 4) Sinais de uma função do 2° grau com duas raízes  e  iguais e concavidade da parábola voltada para baixo.

A partir do gráfico, podemos identificar que:

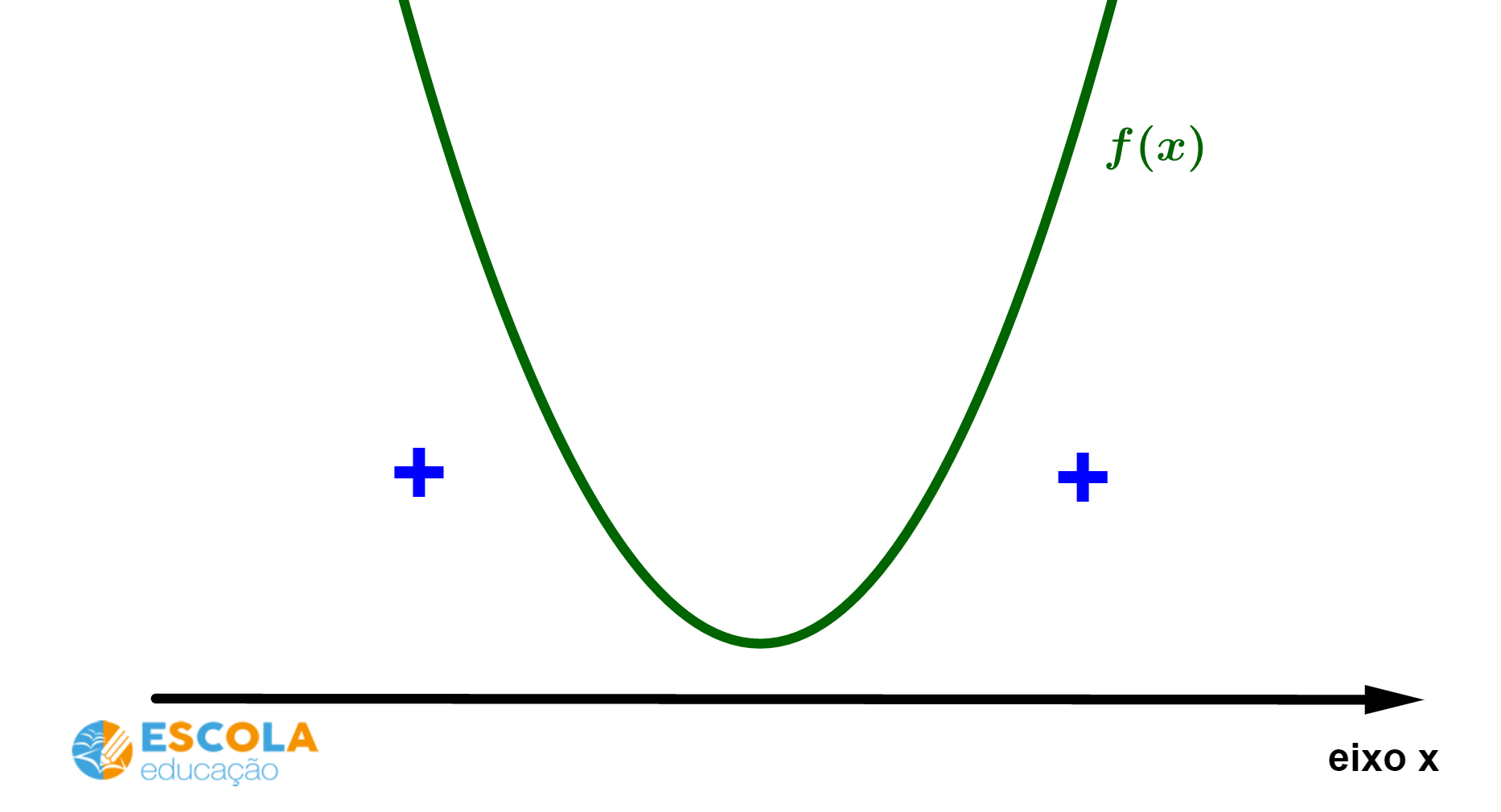
Caso 5) Sinais de uma função do 2° grau sem raízes reais e concavidade da parábola voltada para cima.

Nesse caso, temos f(x) > 0 para qualquer x pertencente aos reais.

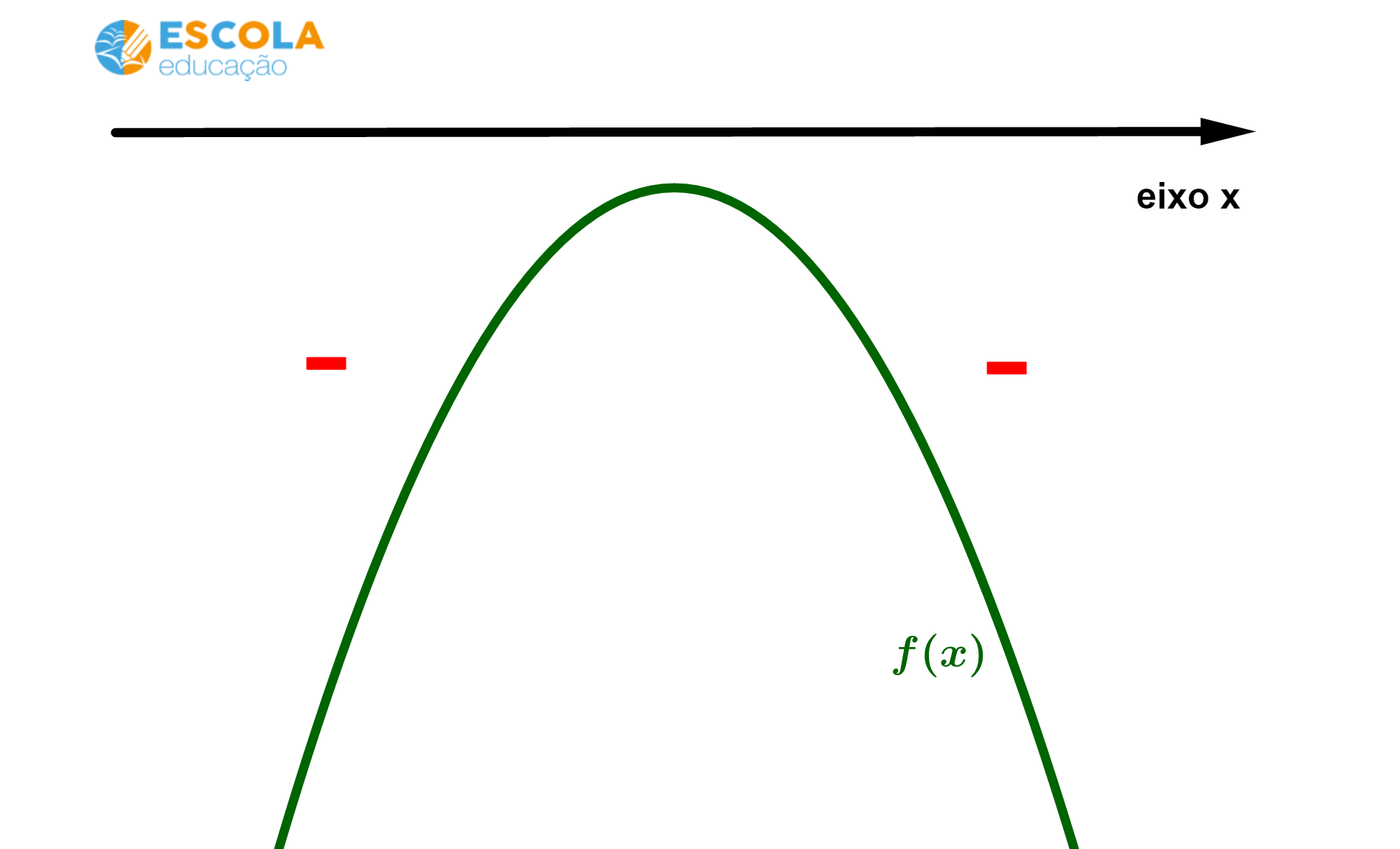
Caso 6) Sinais de uma função do 2° grau sem raízes reais e concavidade da parábola voltada para baixo.

Nesse caso, temos f(x) < 0 para qualquer x pertencente aos reais.

Como verificar a concavidade da parábola

A concavidade da parábola pode ser determinada pelo valor do coeficiente a da função do 2° grau.

• Se a > 0, então a parábola tem concavidade para cima;
• Se a < 0 , então a parábola tem concavidade para baixo.

Como verificar se a parábola intercepta o eixo x

Verificar se a parábola intercepta ou não o eixo x, significa determinar se a função possui ou não raízes e, se possui, quais são elas. Podemos determinar isso, calculando o discriminante: .

• Se  > 0 , a função tem duas raízes reais diferentes e a parábola intercepta o eixo x em dois pontos diferentes.
• Se  = 0, a função tem duas raízes reais iguais, a parábola intercepta o eixo x em um único ponto.
• Se  < 0, a função não tem raízes reais e a parábola não intercepta o eixo x, estando totalmente acima do eixo x se tiver concavidade para cima e totalmente abaixo do eixo x se tiver concavidade para baixo.

Nos dois primeiros casos em que existem raízes, elas podem ser calculadas a partir da fórmula de Bhaskara.

Você também pode se interessar:

• Como fazer o gráfico da função do segundo grau
• Coordenadas do vértice da parábola
• Exercícios de função do primeiro grau (função afim)
• Funções trigonométricas – Seno, cosseno e tangente