Polígonos

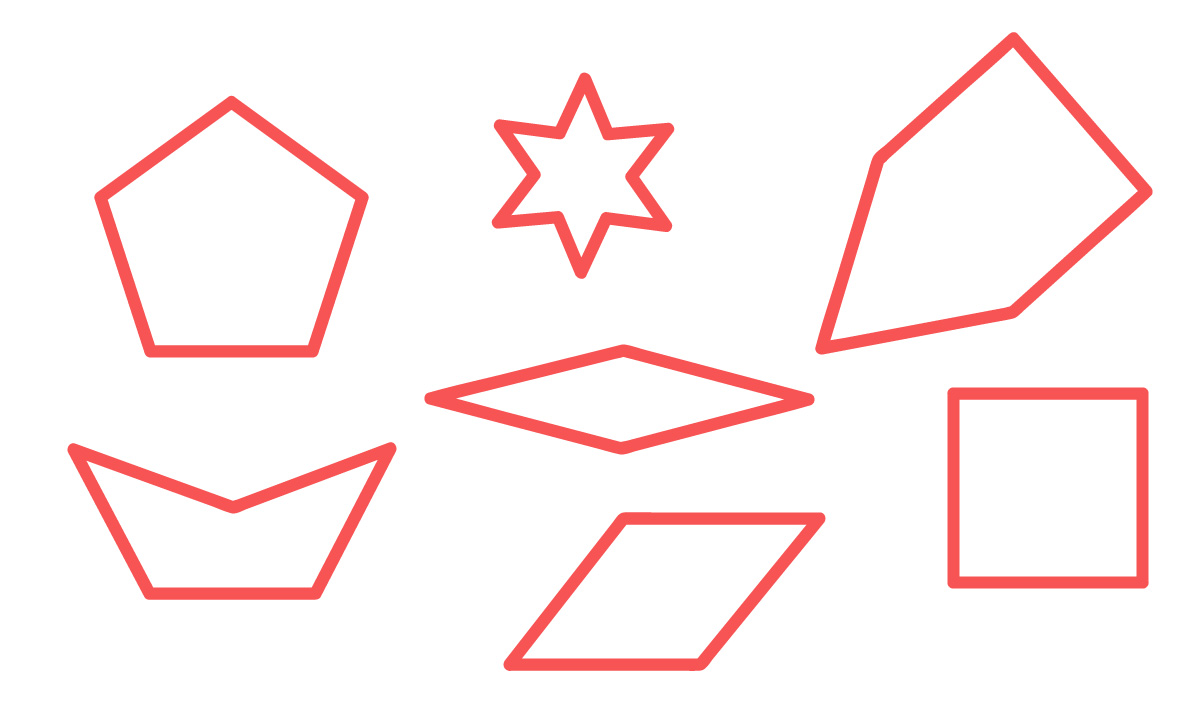
Os polígonos são figuras geométricas planas formadas por uma linha fechada composta apenas por segmentos de reta.

Se a linha que forma um polígono não apresentar nenhum ponto de cruzamento, ou seja, for uma linha simples, temos um polígono simples. Caso contrário, o polígono é chamado de polígono complexo.

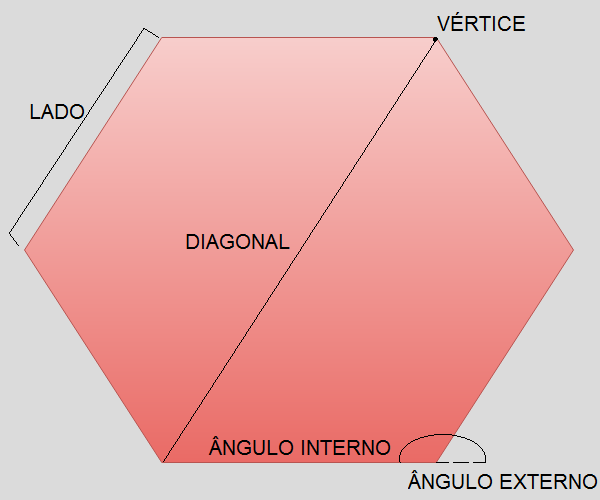
Elementos do polígono

Lados: são os segmentos de reta que formam o polígono.

Vértices: são os pontos de encontro entre dois lados.

Diagonal: é qualquer segmento de reta que passa pelo meio da figura ligando dois vértices.

Ângulos internos: é cada um dos ângulos formados pela junção de dois lados do polígono.

Ângulos externos: são os ângulos formados entre um lado do polígono e o prolongamento do lado consecutivo.

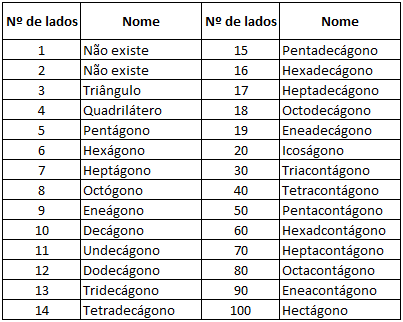
Nomes dos polígonos

Alguns polígonos são nomeados de acordo com o número de lados ou de ângulos que eles possuem. A seguir, temos uma tabela com o nome dos polígonos.

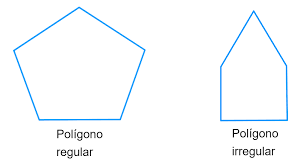
Polígono regular

Um polígono regular é aquele onde todos os lados têm o mesmo tamanho e todos os ângulos internos têm a mesma medida. Caso contrário, o polígono é irregular.

Polígono convexo e côncavo

Temos um polígono côncavo quando for possível desenhar um segmento de reta com ponto de início e fim na região interna do polígono e alguma parte do segmento na região externa do polígono. Se isso não for possível, temos um polígono convexo.

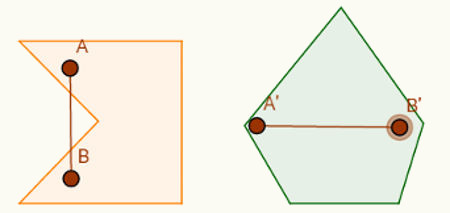
Uma estratégia para identificar um polígono côncavo, é lembrar do jogo do Pac-Man. A região por onde passa o segmento de reta lembra a boca do Pac-Man:

Soma dos ângulos de um polígono

A soma dos ângulos internos de um polígono convexo pode ser obtida a partir da seguinte fórmula:

S = (n – 2) . 180

Onde n é o número de lados do polígono.

Exemplo: Calcular a soma dos ângulos internos de um pentágono convexo.

S = (n – 2) . 180

S = (5 – 2) . 180

S = 3 . 180

S = 540

Logo, a soma dos ângulos internos de um pentágono convexo é 540°.

Já a soma dos ângulos externos de qualquer polígono convexo é igual a 360°.

Número de diagonais de um polígono

O número de diagonais de um polígono pode ser obtido através da seguinte fórmula:

d = [n.(n – 3)] / 2

Onde n é o número de lados do polígono.

Exemplo: Calcular o número de diagonais de um dodecágono (12 lados).

d = [ n.(n – 3)] / 2

d = [12.(12 – 3)] / 2

d = [12. 9] / 2

d = 108 / 2

d = 54

Então, um dodecágono possui 54 diagonais.

Perímetro e área dos polígonos

O perímetro do polígono é dado pela medida do seu contorno, ou seja, a medida da linha que o forma. Assim, para obter o perímetro de um polígono, basta somar a medida de todos os seus lados.

Exemplo: Calcular o perímetro de um quadrado com lado medindo 3 cm.

Perímetro = 3 + 3 + 3 + 3 = 12

Logo, o perímetro desse quadrado é igual a 12 cm.

Enquanto isso, a área do polígono é a medida de sua superfície, então, quando calculamos a área do polígono estamos obtendo a medida do espaço que ele ocupa.

Para saber mais, veja: Área e perímetro.

Para alguns polígonos, existem fórmulas que facilitam o cálculo da área. Para saber mais sobre isso, leia:

• Área do quadrado
• Área do Triângulo
• Área do retângulo
• Área do losango
• Áreas de figuras planas
• Lista de exercícios de área de figuras planas
• Área do trapézio – Tipos de trapézio, como calcular a área e o perímetro de um trapézio