A esfera na geometria espacial
Na geometria espacial, a esfera é classificada como um corpo redondo. Conheça mais sobre a esfera, sua definição e fórmulas.
A geometria espacial é a parte da geometria que estuda as figuras no espaço, isto, em três dimensões.
As figuras tridimensionais também são chamadas de sólidos geométricos e são classificadas em dois grupos: poliedros e corpos redondos.
A esfera é um dos corpos redondos da geometria espacial, assim como cone e cilindro.
Diversos objetos ou coisas que existem possuem o formato de uma esfera, começando pelo planeta no qual vivemos, a Terra.

Dessa forma, o estudo da esfera na geometria espacial é de grande importância e com aplicações em diversas áreas do conhecimento.
Esfera – Figura geométrica espacial
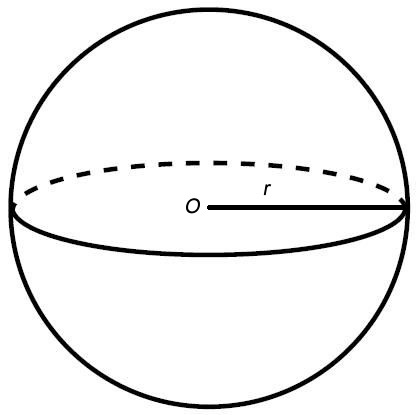
Considere um ponto O no espaço e todos os pontos que estão a uma mesma distância r desse ponto, em todas as direções.
A superfície formada por esse conjunto de pontos é chamada de superfície esférica. A superfície esférica e todo o seu interior constituem uma esfera.
Considere, por exemplo, uma melancia. A casca da melancia é a superfície esférica e a melancia inteira é a esfera.
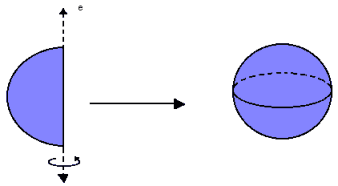
Outra forma de definir a esfera é como a figura geométrica que se forma com a rotação de um semicírculo em torno do seu eixo.
Fórmula da esfera
As principais fórmulas da esfera são da área da superfície e volume.
A área da superfície esférica corresponde à medida da sua superfície e pode ser obtida pela seguinte fórmula:
Em que:
;
: raio da esfera.
Volume da esfera
O volume da esfera corresponde ao espaço ocupado por ela e pode ser calculado com a fórmula a seguir:
Em que:
;
: raio da esfera.
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.