Geometria analítica
Quer entender o que é geometria analítica? O que é estudado, quais as principais fórmulas e conceitos? Confira esse artigo!
Geometria analítica é uma parte da matemática que estuda as figuras geométricas a partir de um ponto de vista algébrico.
Um dos objetivos principais da geometria analítica é reunir técnicas para descrever, com expressões algébricas, as formas geométricas, áreas, volumes, distâncias, pontos de intersecção, posições de retas, ângulos de inclinação, etc.
Uma ferramenta importante na geometria analítica chama-se sistema de coordenadas, por meio do qual é possível localizar pontos, no plano ou no espaço. Dessa forma, os objetos de estudo podem ser visualizados e compreendidos com mais clareza.
Plano cartesiano
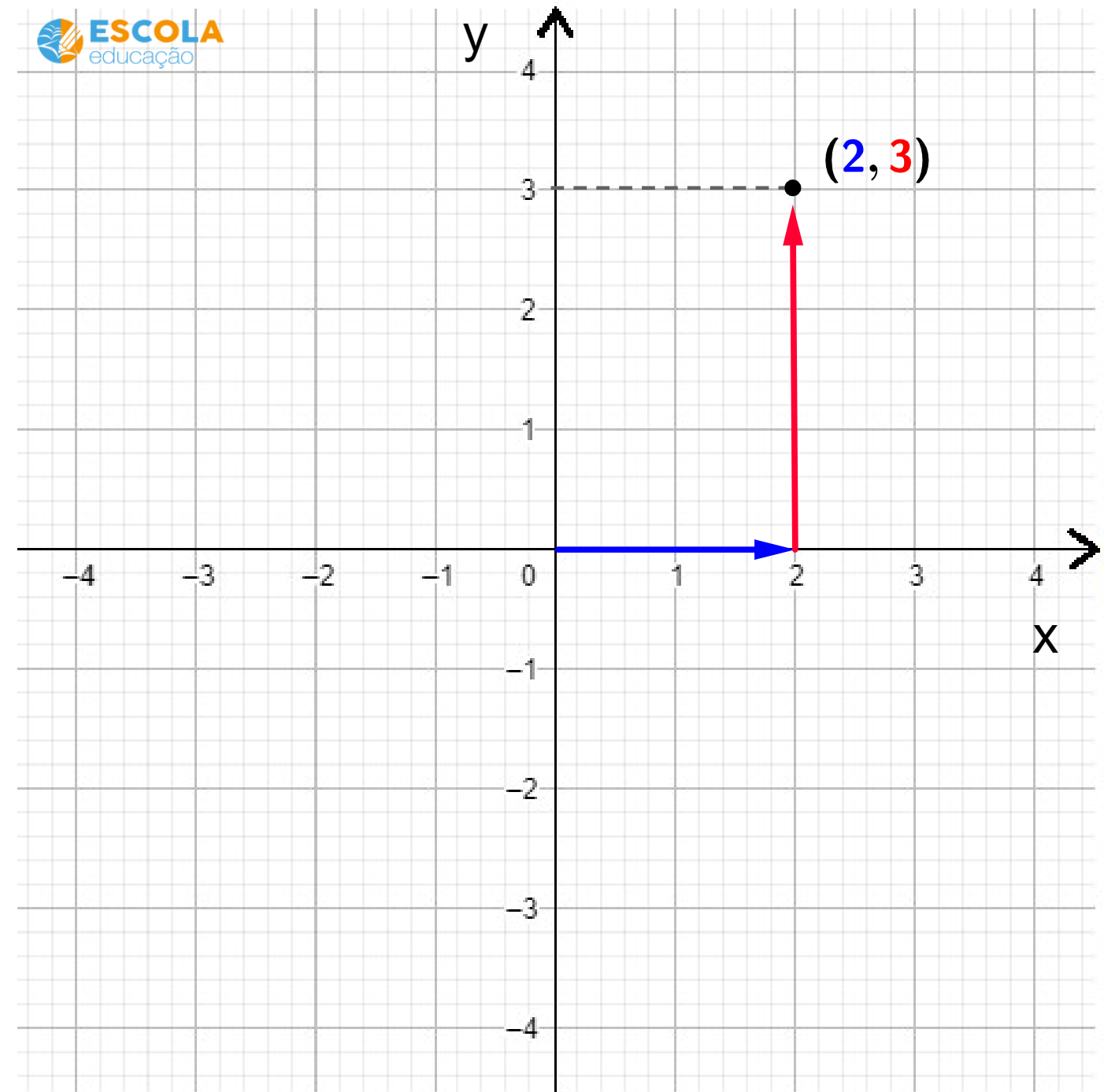
O plano cartesiano é um sistema de coordenadas para localização de pontos no plano, sendo formado por duas retas perpendiculares.
A reta horizontal é chamada de eixo x, ou eixo das abscissas, e a reta vertical é o eixo y, ou eixo das ordenadas.
Quando localizamos vários pontos que pertencem a uma reta, por exemplo, conseguimos traçar o gráfico da reta e entender características importantes dessa reta, como a posição relativa entre ela e outras retas.
Fórmulas de geometria analítica
Veja a seguir as principais fórmulas e expressões de geometria analítica.
a, b e c são constantes calculadas a partir das coordenadas de dois pontos distintos pertencentes à reta.
Coeficiente angular da reta (inclinação):
e
: dois pontos pertencentes à reta.
O ponto de intersecção é a solução do sistema de equações.
: centro da circunferência;
: raio da circunferência.
Equação da elipse:
e
: focos da elipse;
.
Equação da parábola:
: foco da parábola.
Equação da hipérbole:
e
: focos da hipérbole;
.
Você também pode se interessar:
- Áreas de figuras planas
- Reta, semirreta e segmento de reta
- Planificação de sólidos geométricos
- Exercícios sobre equação da circunferência

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.