Identidades trigonométricas

As identidades trigonométricas possibilitam simplificar e resolver muitos cálculos. Veja quais são as identidades fundamentais e as relações derivadas.

Por Elainy Marciano Publicado em 06/11/2020 - 18:00

As identidades trigonométricas são relações que existem entre as funções trigonométricas e que são verdadeiras para todos os valores do domínio das funções envolvidas.

As identidades trigonométricas também são chamadas de relações trigonométricas e podem ser classificadas em fundamentais e derivadas ou recorrentes.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Identidades trigonométricas fundamentais

A primeira identidade ou relação fundamental também é conhecida como relação pitagórica, pois deriva da aplicação direta do teorema de Pitágoras no círculo trigonométrico.

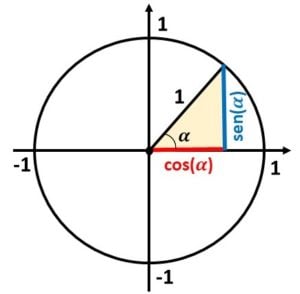
No triângulo retângulo, a soma dos quadrados dos catetos é igual à hipotenusa ao quadrado. Observando a figura, os catetos são o seno e o cosseno do ângulo, e a hipotenusa é igual ao raio, que é 1.

Assim, obtém-se a primeira identidade fundamental.

1ª Identidade fundamental

$\dpi{120} \boldsymbol{sen^2\, (\alpha) +cos^2\, (\alpha) = 1}$

A partir dessa identidade, temos duas relações muito utilizadas em cálculos de trigonometria:

$\dpi{120} \boldsymbol{sen^2\, (\alpha) = 1-cos^2\, (\alpha) }$

$\dpi{120} \boldsymbol{ cos^2\, (\alpha) = 1-sen^2\, (\alpha)}$

Veja agora, outras identidades trigonométricas que são fundamentais e relacionam as funções tangente, secante, cossecante e cotangente.

A tangente de um ângulo corresponde ao cateto oposto ao ângulo dividido pelo cateto adjacente ao ângulo. Dessa forma, a tangente de $\dpi{120} \alpha$ é igual ao seno de $\dpi{120} \alpha$ dividido pelo cosseno de $\dpi{120} \alpha$ .

2ª Identidade fundamental

$\dpi{120} \boldsymbol{tan(\alpha)= \frac{sen(\alpha)}{cos(\alpha)}}$

A secante de um ângulo $\dpi{120} \alpha$ é igual ao inverso da função cosseno do ângulo $\dpi{120} \alpha$ .

3ª Identidade fundamental

$\dpi{120} \boldsymbol{sec(\alpha)= \frac{1}{cos(\alpha)}}$

A cossecante de um ângulo $\dpi{120} \alpha$ é igual ao inverso da função seno do ângulo $\dpi{120} \alpha$ .

4ª Identidade fundamental

$\dpi{120} \boldsymbol{csc(\alpha)= \frac{1}{sen(\alpha)}}$

A cotangente de um ângulo $\dpi{120} \alpha$ é igual ao inverso da função tangente do ângulo $\dpi{120} \alpha$ .

5ª Identidade fundamental

$\dpi{120} \boldsymbol{cot(\alpha)= \frac{1}{tan(\alpha)}}$

Relações trigonométricas derivadas

A partir das relações fundamentais, outras relações podem ser obtidas e elas são chamadas de relações derivadas ou relações decorrentes.

Dividindo todos os termos da primeira identidade fundamental $\dpi{120} sen^2\, (\alpha) +cos^2\, (\alpha) = 1$ por $\dpi{120} cos^2(\alpha)$ , temos que:

$\dpi{120} \frac{sen^2\, (\alpha)}{cos^2 \, (\alpha)} + \frac{cos^2\, (\alpha)}{cos^2 \, (\alpha)} = \frac{1}{cos^2 \, (\alpha)}$

$\dpi{120} \Rightarrow \left ( \frac{sen\, (\alpha)}{cos\, (\alpha)}\right )^2 + 1 = \left ( \frac{1}{cos \, (\alpha)}\right )^2$

$\dpi{120} \Rightarrow tan^2(\alpha) + 1 = sec^2 (\alpha)$

E, assim, obtemos a primeira relação derivada.

1ª Relação derivada

$\dpi{120} \boldsymbol{sec^2(\alpha)= tan^2(\alpha)+1 }$

Por outro lado, dividindo todos os termos da identidade fundamental $\dpi{120} sen^2\, (\alpha) +cos^2\, (\alpha) = 1$ por $\dpi{120} sen^2(\alpha)$ , temos que: