O que é geometria plana?

A geometria plana é o campo da matemática que estuda as formas geométricas de até duas dimensões, ou seja, aquelas que podem apresentar largura e comprimento, mas não têm profundidade.

Em homenagem a um grande matemático chamado Euclides de Alexandria, considerado o “pai da geometria”, a geometria plana também é conhecida por geometria euclidiana.

O desenvolvimento da geometria plana, tanto em relação aos conceitos quanto às propriedades, como o próprio nome sugere, é feito a partir de uma estrutura chamada plano.

O que é o plano?

O plano é uma região bidimensional, com largura e comprimento, que permite o estudo das figuras geométricas planas.

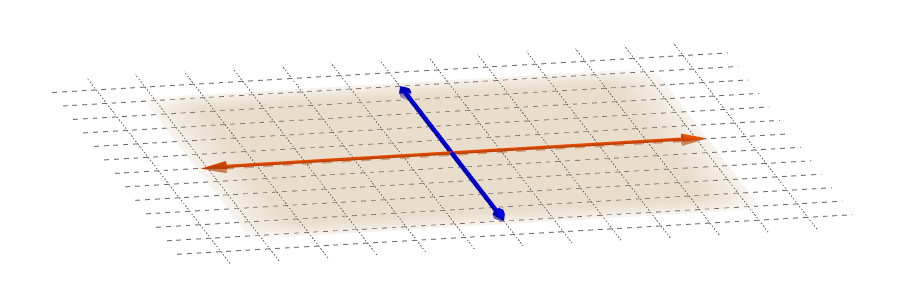
Um plano pode ser determinado por três pontos não alinhados, uma reta e um ponto fora dela ou duas retas que se interceptam, como é apresentado na figura abaixo.

Figuras geométricas planas

As figuras geométricas planas são objetos de estudo da geometria plana. Entre elas, destacam-se os círculos, quadrados, retângulos e triângulos.

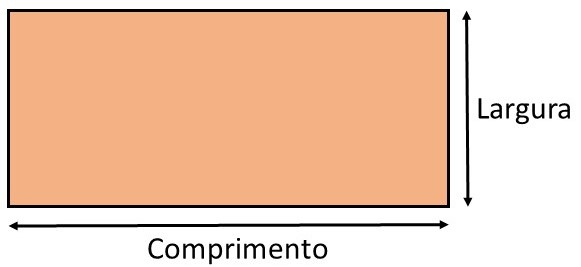
Todas as figuras planas apresentam duas dimensões: largura e comprimento. Veja o exemplo no retângulo:

As figuras planas podem ser classificadas em dois grupos principais: os polígonos e os não polígonos.

Polígonos

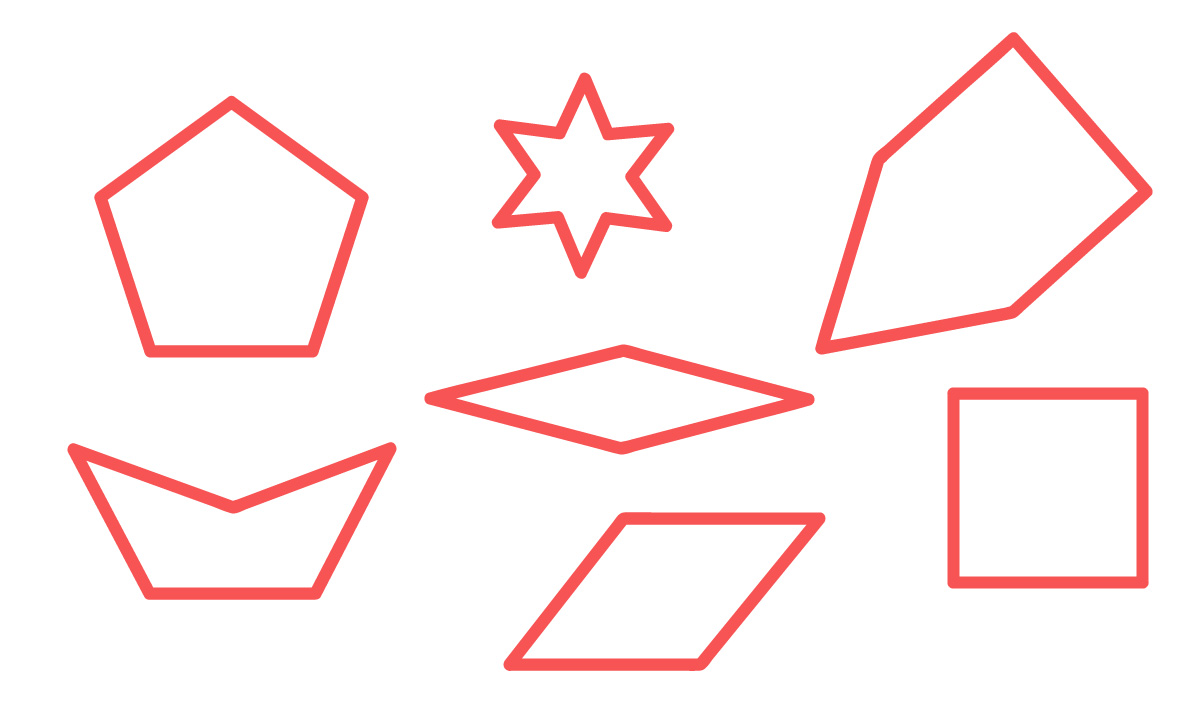
Os polígonos são as figuras planas formadas por uma linha fechada, que não se cruza e cujos lados são apenas segmentos de reta.

Em outras palavras, polígonos não possuem curvatura, são aquelas figuras geométricas que desenhamos apenas com a régua, já que segmentos de reta são pequenas partes de uma reta.

Não polígonos

As figuras planas que não se classificam como polígonos são chamadas de não polígonos. São figuras cuja linha é aberta, apresentam algum ponto de cruzamento ou algum tipo de curvatura.

Você também pode se interessar:

• Geometria espacial
• Geometria analítica
• Geometria fractal
• Áreas de figuras planas
• Perímetro de figuras planas