Sólidos de Platão
Conheça os sólidos geométricos associados aos quatro elementos básicos e ao universo pelo grande filósofo Platão.
Em geometria, os sólidos geométricos são figuras que possuem três dimensões: altura, largura e profundidade, ou seja, são figuras espaciais. Entre esse tipo de figuras, estão aquelas conhecidas como sólidos de Platão.
Platão (427–347 a.C.) foi um grande filósofo e matemático que viveu na Grécia Antiga e que se consagrou como um dos maiores pensadores da história humana.
Para Platão, quatro elementos básicos, terra, fogo, ar e água, formavam o universo, que seria o quinto elemento, e cada um desses elementos poderia ser associado a uma forma geométrica próxima da perfeição, em específico, a um sólido geométrico regular.
Sólidos de Platão
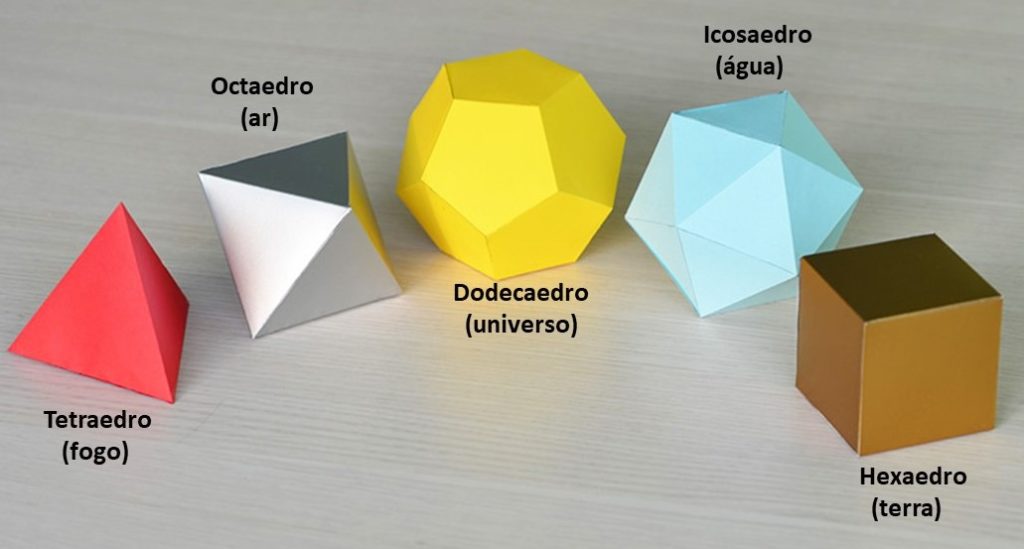
Os sólidos de Platão são: tetraedro, hexaedro, octaedro, icosaedro e dodecaedro.
Todos esses sólidos pertencem ao grupo dos poliedros, que são os sólidos geométricos formados por faces planas poligonais, vértices e arestas.
Conheça as características principais de cada um dos sólidos de Platão, ou poliedros de Platão.
1 — Tetraedro
O tetraedro é um poliedro formado por 4 faces que são triângulos equiláteros, 4 vértices e 6 arestas. Platão associou o tetraedro ao fogo.
2 — Hexaedro
O hexaedro, mais conhecido como cubo, é um poliedro formado por 6 faces quadradas, 8 vértices e 12 arestas. Esse poliedro foi associado ao elemento terra.
3 — Octaedro
O octaedro é um poliedro formado por 8 faces que são triângulos equiláteros, 12 arestas e 6 vértices. Ele foi associado ao elemento ar.
4 — Icosaedro
O icosaedro é um poliedro formado por 20 faces que são triângulos equiláteros, 30 arestas e 12 vértices. O icosaedro foi associado à água.
5 — Dodecaedro
O dodecaedro é um poliedro formado por 12 faces que são pentágonos, 30 arestas e 20 vértices. O dodecaedro foi associado, por Platão, ao quinto elemento, o universo.
Fórmula de Euler
Para os poliedros convexos, dentre os quais se encontram os poliedros de Platão, o número de faces, de vértices e de arestas estão relacionados pela seguinte fórmula:
Nº de faces + Nº de vértices – Nº de arestas = 2
Essa fórmula é chamada de fórmula de Euler.
Exemplo: Já sabemos que o cubo possui 6 faces, 8 vértices e 12 arestas. Vamos conferir que a fórmula de Euler é verdadeira para o cubo, calculando 6 + 8 – 12 e obtendo como resultado o número 2:
6 + 8 – 12 = 14 – 12 = 2
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.