O que é geometria?
Saiba o que é geometria, quais são conceitos básicos, suas classificações e divisões.
A palavra geometria tem origem grega, geo significa “terra”, e metria significa “medir”, por isso, essa palavra é usada para designar um dos três principais ramos da matemática.
Conceitos básicos da geometria
A geometria é constituída a partir de alguns fundamentos que, apesar de não possuírem uma definição específica, são muito importantes.
A seguir, conheça os conceitos básicos da geometria.
- Ponto: é uma figura bem simples e intuitiva que não possui dimensões.
- Reta: é uma figura unidimensional formada por infinitos pontos alinhados. Ela não tem começo e nem fim.
- Semirreta: é uma parte da reta. Ela possui começo, mas não possui fim.
- Segmento de reta: é uma parte da reta. Ela possui começo e fim.
- Plano: é uma região ilimitada, que permite a construção de formas geométricas com até duas dimensões.
- Espaço: é uma região ilimitada, que permite a construção de formas geométricas com até três dimensões.
- Ângulo: é uma região do plano formada entre duas semirretas de mesma origem.
Formas geométricas
As formas geométricas são classificadas de acordo com as dimensões que possuem.
O ponto é uma figura sem dimensão, a reta é uma figura unidimensional, e existem as figuras bidimensionais, chamadas de figuras planas, e as figuras tridimensionais, chamadas de figuras espaciais.
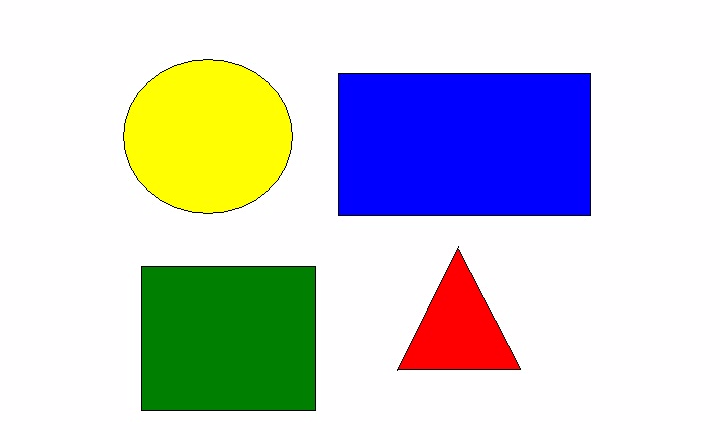
Figuras geométricas planas
As figuras geométricas planas são as figuras de duas dimensões, elas possuem comprimento e largura e podem ser desenvolvidas e estudadas a partir do plano.
Entre as figuras planas, destacam-se os:
- Quadrados;
- Retângulos;
- Paralelogramos;
- Triângulos;
- Círculos;
- Pentágonos,
- Hexágonos;
- Trapézios;
- Losangos.
As figuras geométricas planas se classificam como polígonos ou não polígonos. O quadrado é um exemplo de polígono e o círculo é um exemplo de não polígono.
Figuras geométricas espaciais
As figuras geométricas espaciais também são chamadas de sólidos geométricos e são aquelas que apresentam três dimensões: comprimento, largura e profundidade. Esse tipo de forma geométrica é estudada no espaço.
Entre as principais formas geométricas espaciais, destacam-se os/as:
As figuras espaciais se dividem em dois grupos: poliedros e corpos redondos. O cubo é um exemplo de poliedro e a esfera é um exemplo de corpo redondo.

Divisões da geometria
A geometria é dividida de acordo com os diferentes objetos de estudo. Há a geometria plana, geometria espacial, geometria analítica e geometria fractal.
Geometria plana é a parte da geometria que se destina ao estudo das figuras geométricas no plano, ou seja, em duas dimensões: comprimento e largura.
Nesse caso, as figuras geométricas planas assim como suas propriedades, cálculo de perímetros e áreas são estudados na geometria plana.
Geometria espacial é a parte da geometria que se destina ao estudo das figuras geométricas no espaço, ou seja, em três dimensões: comprimento, largura e profundidade.
Portanto, os sólidos geométricos e suas propriedades, tais como volumes, são estudados na geometria espacial.
Geometria analítica é a parte da matemática que se destina ao estudo das figuras geométricas a partir de expressões algébricas, descrevendo-as através de um sistema de coordenadas, o plano cartesiano.
Distâncias entre pontos, posições relativas de figuras, ângulos de inclinação, entre outros, são estudados na geometria analítica.
Geometria fractal
Geometria fractal é a parte da geometria que se destina ao estudo de fractais.
Os fractais são estruturas geométricas belíssimas que apresentam um padrão de repetição infinito, onde cada pequena parte da figura se assemelha com a figura toda.

Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.