Solução da inequação fundamental sen x > k
Veja como é a solução da inequação fundamental sen x > k, quando k é um valor positivo e quando é um valor negativo.
Uma inequação trigonométrica é uma desigualdade que envolve ao menos uma função trigonométrica da incógnita. Lembre-se que uma desigualdade é dada por duas sentenças e um dos símbolos >, <, ≥ ou ≤, nunca o símbolo de igualdade (=).
Entre as inequações trigonométricas há aquelas que são chamadas de fundamentais: sen x > k, sen x < k, cos x > k, cos x < k, tan x > k e tan x < k. Elas são chamadas assim, pois qualquer inequação trigonométrica sempre pode ser reduzida a uma delas.
Cada uma das inequações fundamentais possui uma solução diferente. Vamos mostrar como é a solução da inequação fundamental sen x > k.
Solução da inequação fundamental sen x > k
Para entender a solução da inequação fundamental sen x > k, vamos considerar a representação no círculo trigonométrico.
Lembre-se de que o círculo trigonométrico é um círculo de raio 1 e que os valores do seno de um arco correspondem aos valores do eixo y (eixo das ordenadas). Portanto, k é um valor entre -1 e 1 no eixo y. Já o valor de x corresponde ao arco formado no círculo trigonométrico.
Assim, vamos considerar dois casos, quando k é positivo e quando k é negativo, para determinar a solução da inequação sen x > k.
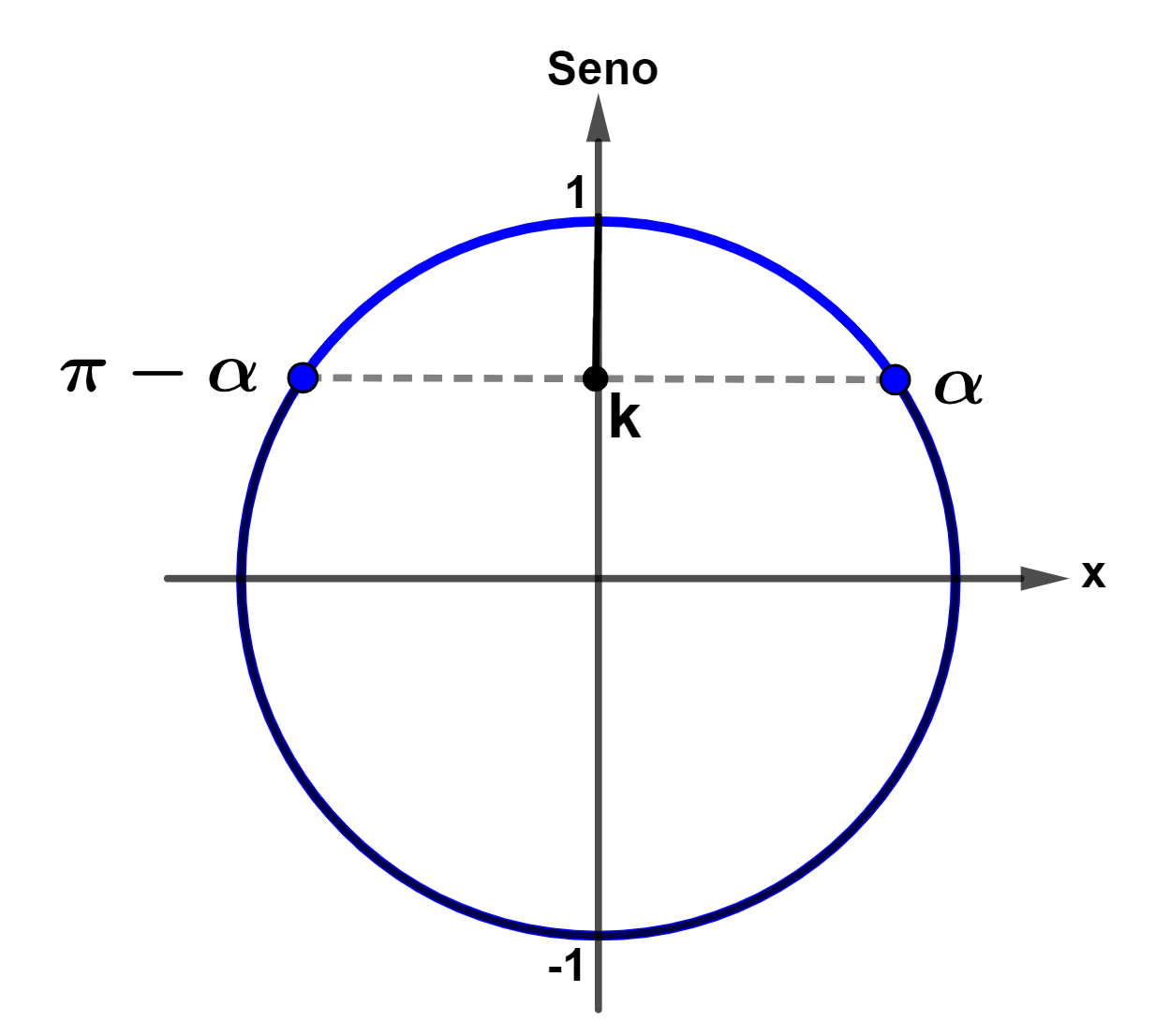
Suponha um valor de k qualquer no intervalo [0,1] e um arco α no 1º quadrante de forma que sen α = k. Consequentemente, o seno do ângulo suplementar ao ângulo α, que é um ângulo obtuso no 2º quadrante, também será igual a k, ou seja, sen (π -α) = k.
Veja a ilustração:
Então, para que sen x > k, devemos considerar que x seja um arco maior que α e menor que π -α. Portanto, a solução é:
S = {x ∈ ℜ| α < x < π – α}
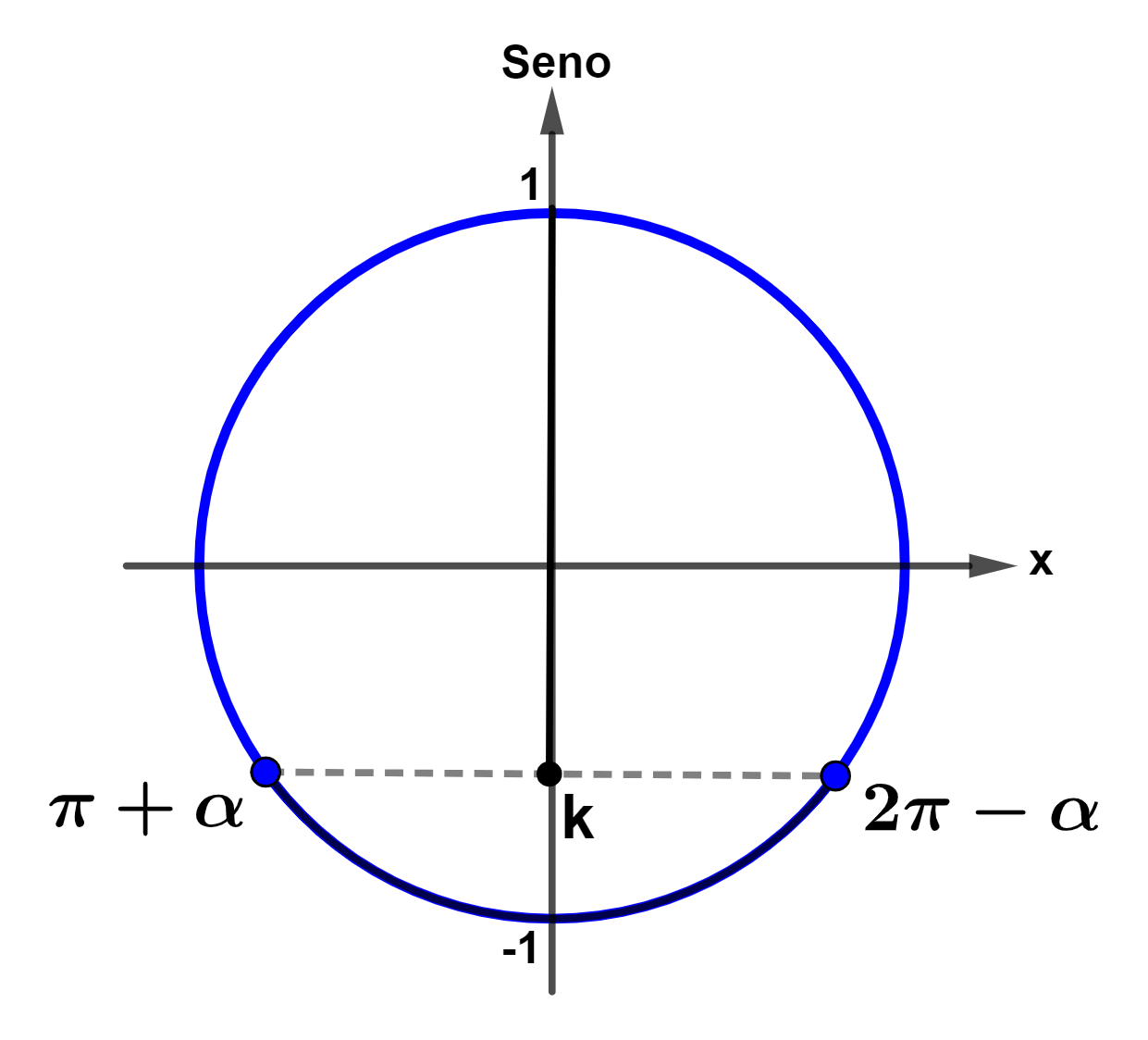
Suponha um valor de k qualquer no intervalo [-1,0) de forma que sen (π + α) = k e sen (2π – α) = k.
Veja a ilustração:
Então, para que sen x > k, devemos considerar que x seja um arco maior que (2π – α) e menor que (π + α). Portanto, a solução é:
S = {x ∈ ℜ| 2π – α < x < π + α}
Exemplo: Para 0 ≤ x ≤ 2π, determine a solução da inequação sen x > 0,5.
Nesse caso, k é um valor positivo, então, vamos considerar a solução conforme o caso 1.
Primeiro, calculamos sen x = 0,5, ou seja, determinamos para qual arco x o seno é igual a 0,5.
A partir da tabela trigonométrica ou de uma calculadora, podemos ver que é o arco de 30°, pois sen 30° = 1/2 = 0,5.
Em radianos, o arco correspondente é π/6. Logo, na solução, temos α = π/6.
S = {x ∈ ℜ| α < x < π – α}
⇒ S = {x ∈ ℜ| π/6 < x < π – π/6}
⇒ S = {x ∈ ℜ| π/6 < x < 5π/6}
Você também pode se interessar:
- Utilizando as relações trigonométricas
- Transformações trigonométricas
- Funções trigonométricas do arco metade
- Funções trigonométricas do arco duplo

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.