Taxa de variação da função do 1º grau

Saiba o que é entenda como calcular a taxa de variação média e instantânea de uma função do 1º grau. Veja exemplos!

Por Elainy Marciano Publicado em 04/12/2020 - 17:03

A taxa de variação é um conceito muito importante no estudo das funções. Para compreender o que é a taxa de variação da função do 1º grau, relembre algumas características desse tipo de função.

Função do 1º grau

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

A função do 1º grau também é chamada de função afim, sendo da forma $\dpi{120} \small \mathbf{f(x) = ax + b}$ , onde $\dpi{120} \small \mathbf{a}$ e $\dpi{120} \small \mathbf{b}$ são dois números reais.

O gráfico da função do 1º grau é sempre uma reta, cuja inclinação é determinada pelo valor $\dpi{120} \small \mathbf{a}$ , que é chamado de coeficiente angular. Já o valor $\dpi{120} \small \mathbf{b}$ é o valor onde a reta intercepta o eixo y no gráfico, sendo chamado de coeficiente linear.

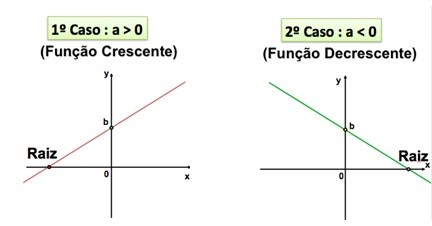
O comportamento da função do 1º grau varia conforme o coeficiente angular, por exemplo, se $\dpi{120} \small \mathbf{a>0}$ , a função é crescente, mas se $\dpi{120} \small \mathbf{a<0}$ , a função é decrescente.

O coeficiente angular é um valor muito importante na função do 1º grau e também é chamado de taxa de variação média da função do 1º grau.

Taxa de variação média

A taxa de variação média (TVM) da função do 1º grau é obtida a partir de dois pontos pertencentes a função, $\dpi{120} \small \mathbf{P_1(x_1,y_1)}$ e $\dpi{120} \small \mathbf{P_2(x_2,y_2)}$ , ela corresponde à razão entre a variação dos valores de y e a variação dos valores de x.

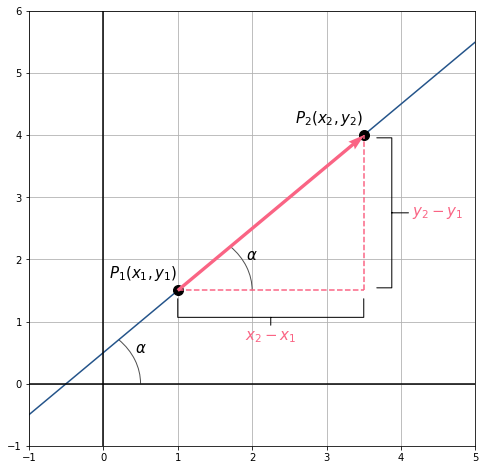
Taxa de variação média da função do 1º grau:

$\dpi{120} \small \mathbf{TVM = \frac{y_2 - y_1}{x_2 - x_1}}$

Portanto, a taxa de variação média da função do 1º grau nada mais é do que o coeficiente angular da função, ou ainda, a tangente do ângulo de inclinação da reta.

Exemplo 1: Na função f(x) = 3x + 4, o coeficiente angular é 3, que é o valor que está sendo multiplicado por x, então, a taxa de variação média da função é 3.

Exemplo 2: Dados dois pontos (0, 2) e (2,4), o coeficiente angular da reta que passa por esses dois pontos ou taxa de variação média é dado por:

$\dpi{120} \small \mathrm{a= TVM = \frac{4-2}{2 - 0 } = \frac{2}{2} = 1}$

A partir do coeficiente angular (a) e de um ponto qualquer, podemos determinar a equação da reta:

$\dpi{120} \small \mathrm{y - y_0 = a(x - x_0)}$

Sendo a = 1 e usando o ponto (0,2), temos:

$\dpi{120} \small \mathrm{y - 2 = 1(x - 0)}$

$\dpi{120} \small \mathrm{y - 2 = x}$

$\dpi{120} \small \mathrm{y = x+ 2}$

Portanto, temos a função correspondente y = f(x) = x + 2.

Taxa de variação instantânea

A taxa de variação instantânea, mais conhecida como derivada de uma função, é uma definição normalmente vista nos cursos superiores da área de exatas, nas disciplinas de Cálculo.

A seguir, apresentamos uma breve descrição do que seria a taxa de variação instantânea.

A ideia de calcular a taxa de variação instantânea é a de ir considerando dois pontos cada vez mais próximos um do outro, de forma que a variação entre eles seja bem pequena, quase igual a zero.

Considerando que $\dpi{120} \small \mathrm{y_1 = f(x_1)}$ e que $\dpi{120} \small \mathrm{y_2 = f(x_2)}$ , então, a taxa de variação instantânea ou derivada da função pode ser definida da seguinte forma:

$\dpi{120} \small \mathbf{f'(x)=\lim_{(x_2 - x_1)\rightarrow 0}\frac{f(x_2) - f(x_1)}{x_2 - x_1}}$

Ou, ainda, se considerarmos $\dpi{120} \small \mathrm{x_1 = x}$ , um ponto genérico, e $\dpi{120} \small \mathrm{x_2 = x + h}$ , onde h é um valor bem próximo de zero, então, temos:

$\dpi{120} \small \mathbf{f'(x)=\lim_{h\rightarrow 0}\frac{f(x + h) - f(x)}{h}}$

A taxa de variação pode ser calculada a partir do limite, ou seja, pela definição formal. Mas, além disso, existem algumas regras de derivação, que são regras que nos permitem calcular derivadas de funções mais comuns, de uma forma bem prática. Veja algumas dessas regras:

Se $\dpi{120} \small \mathrm{f(x) = c}$ , sendo c uma constante, então, $\dpi{120} \small \mathrm{f'(x) = 0}$ .
Se $\dpi{120} \small \mathrm{f(x) = cx}$ , então, $\dpi{120} \small \mathrm{f'(x) = c}$ .

Exemplo: Usando essas suas regras de derivação acima, a taxa de variação instantânea ou derivada da função f(x) = – 5x + 1 é f'(x) = -5.

Você também pode se interessar:

Cálculo Funções