Triângulo isósceles

Saiba o que é um triângulo isósceles, quais as principais propriedades, fórmula da altura, área e perímetro e classificações quanto aos ângulos.

Por Elainy Marciano Publicado em 21/07/2020 - 16:15

Qualquer triângulo que possua dois lados de mesma medida é chamado de triângulo isósceles.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

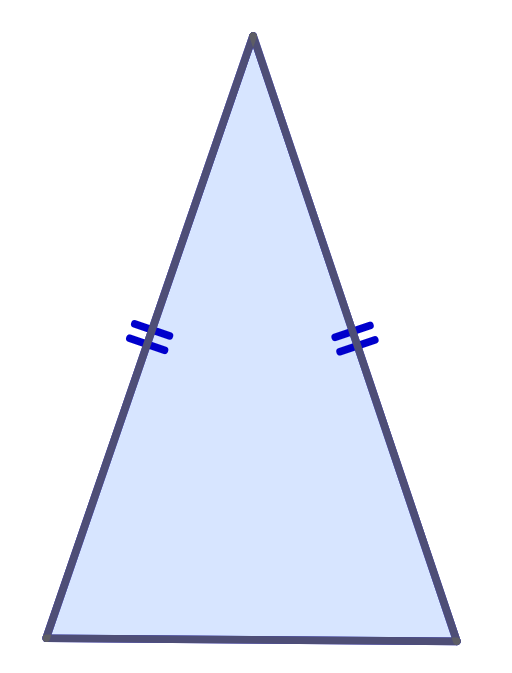
Portanto, triângulo isósceles é uma das possíveis classificações dos triângulos em relação aos lados.

Além de isósceles, os triângulos podem ser, ainda, equiláteros ou escalenos.

Triângulo equilátero: possui os três lados de mesma medida;
Triângulo escaleno: possui os três lados com medidas diferentes.

Propriedades do triângulo isósceles

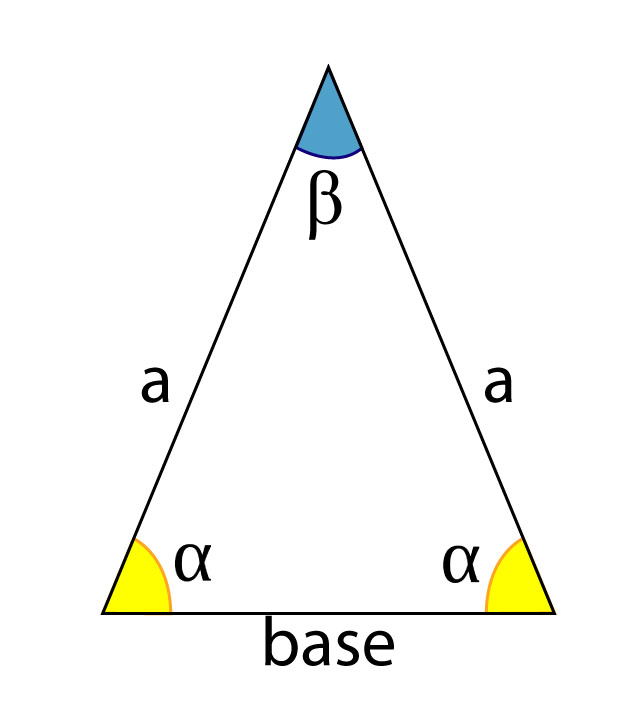
Em um triângulo isósceles, o lado com medida diferente é chamado de base. O ângulo oposto a base é chamado de ângulo do vértice ( $\dpi{120} \beta$ ). Os outros dois ângulos são os ângulos da base ( $\dpi{120} \alpha$ ).

Dito isso, vamos ver quais são as características ou propriedades dos triângulos isósceles.

Propriedade 1: Os ângulos da base de um triângulo isósceles são congruentes, eles têm a mesma medida.

Uma vez que a soma dos ângulos de um triângulo é sempre igual a 180°, então, por essa propriedade do triângulo isósceles, temos:

$\dpi{120} \alpha + \alpha + \beta = 180^{\circ}$

$\dpi{120} \Rightarrow 2 \alpha + \beta = 180^{\circ}$

$\dpi{120} \Rightarrow \beta = 180^{\circ} - 2a$

$\dpi{120} \Rightarrow \alpha= \frac{180^{\circ} - \beta}{2}$

Propriedade 2: Em qualquer triângulo isósceles, a altura relativa à base é igual à mediana e à bissetriz do ângulo do vértice.

A altura relativa ao lado de um triângulo corresponde sempre a um segmento de reta perpendicular a esse lado do triângulo.

Observe, que no triângulo isósceles, a altura relativa à base divide o triângulo em dois triângulos retângulos, que possuem lados e ângulos correspondentes de mesma medida.

Altura do triângulo isósceles

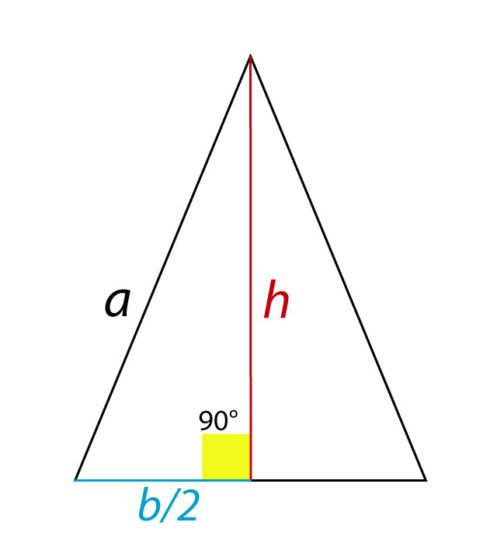
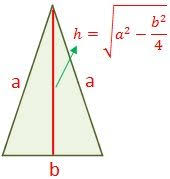
Para determinar a altura do triângulo isósceles, vamos utilizar o teorema de Pitágoras.

Temos:

hipotenusa = $\dpi{120} a$
cateto oposto = h
cateto adjacente = $\dpi{120} b/2$

$\dpi{120} a^2 = h^2 + \bigg(\frac{b}{2}\bigg)^2$

$\dpi{120} \Rightarrow h^2 = a^2 - \bigg(\frac{b}{2}\bigg)^2$

$\dpi{120} \Rightarrow h^2 = a^2 - \frac{b^2}{4}$

$\dpi{120} \Rightarrow h = \sqrt{a^2 - \frac{b^2}{4}}$

Veja a representação:

Perímetro do triângulo isósceles

O perímetro de um triângulo qualquer é dado pela soma das medidas dos três lados.

Portanto, a fórmula do perímetro do triângulo isósceles é:

$\dpi{120} P = a + a + b = 2a + b$

Em que $\dpi{120} a$ é a medida dos lados iguais e $\dpi{120} b$ é a medida do lado diferente (base) do triângulo.

Área do triângulo isósceles

A área do triângulo consiste no produto da medida da base pela altura, dividido por 2. Assim, a área de qualquer triângulo pode ser obtida pela seguinte fórmula:

$\dpi{120} A = \frac{base \times altura}{2}$

Então, para determinar a área do triângulo isósceles, precisamos da medida da base (lado diferente) e a medida da altura relativa à base.

Classificação dos triângulos em relação aos ângulos

Além de ser classificado quanto aos lados, um triângulo também pode ser classificado com relação às medidas dos seus ângulos internos.

Triângulo retângulo: possui um ângulo de 90° (ângulo reto);
Triângulo acutângulo: possui três ângulos menores que 90°;
Triângulo obtusângulo: possui um ângulo maior que 90°.

Você também pode se interessar: