Sistemas lineares
Conheça os métodos para resolver sistemas com duas, três ou mais equações lineares. Veja como classificar esses sistemas!
As equações lineares são equações da forma , em que
são coeficientes da equação,
são incógnitas e
é um valor numérico chamado de termo independente.
Exemplo de equação linear:
é uma equação linear com três incógnitas.
De modo geral, um sistema linear com n equações tem a seguinte forma:
Exemplos de sistemas lineares:
→ Sistema linear com duas equações.
→ Sistema linear com três equações.
Resolução de sistemas lineares
A resolução de sistemas lineares é dada pelo conjunto de valores numéricos que satisfazem todas as equações simultaneamente.
Exemplo: No sistema , os valores de
e
que são satisfazem as duas equações são:
e
.
Veja que se substituirmos esses valores no primeiro lado da igualdade, obtemos o termo independente nas duas equações:
Portanto, a solução do sistema corresponde aos valores das incógnitas que tornam verdadeiras ambas as equações do sistema.
Classificação de sistemas lineares
Um sistema linear pode ser classificado em três diferentes tipos, em relação à quantidade de soluções que possui: possível determinado, possível indeterminado ou impossível.
- Sistema possível e determinado (SPD): é um sistema que possui uma única solução;
- Sistema possível e indeterminado (SPI): é um sistema que possui infinitas soluções;
- Sistema impossível (SI): é um sistema que não possui solução.
Se um sistema linear possuir o mesmo número de incógnitas e equações, podemos determinar se ele possui uma única solução, ou não, bastando escrever o sistema na forma matricial e calcular o determinante.
Sistemas lineares de duas equações
Para resolver sistemas lineares de duas equações, podemos utilizar três métodos diferentes: método da adição, método da substituição e método da comparação.
Método da adição
No método da adição, somamos as equações buscando o cancelamento de termos opostos (um positivo e um negativo), para eliminar uma das incógnitas. Por fim, resolvemos uma equação com uma só incógnita.
Método da substituição
No método da substituição, isolamos uma das incógnitas em uma das equações e substituímos o seu valor na outra equação. Dessa forma, obtemos uma equação com uma só incógnita e podemos resolvê-la.
Método da comparação
No método da comparação, escolhemos uma das incógnitas e isolamos ela nas duas equações. Por fim, fazemos a comparação entre as duas igualdades obtidas, determinando o valor da outra incógnita.
Em todos os três métodos, após determinar a primeira incógnita, a segunda incógnita é determinada substituindo-se o valor da primeira incógnita em qualquer uma das equações do sistema.
Exemplo: Veja como obtemos a solução do sistema .
Vamos utilizar o método da substituição:
1º passo) Isolamos a incógnita na primeira equação:
2º passo) Substituímos por
na segunda equação:
3º passo) Resolvemos a equação do 1º grau obtida:
4º passo) Substituímos por -2 em na primeira equação:
5º passo) Resolvemos a equação do 1º grau obtida:
Então, obtemos a solução . Com os outros dois métodos essa mesma solução deve ser encontrada.
Sistemas lineares de três equações
Para resolver sistemas lineares com três ou mais equações, podemos utilizar alguns métodos diferentes, como a Regra de Cramer e o método do escalonamento da matriz associada.
Uma observação importante é que esses métodos também podem ser usados para resolver sistemas lineares com duas equações. Contudo, é mais simples e usual utilizar os métodos que vimos anteriormente.
Regra de Cramer
A Regra de Cramer é um método que permite resolver sistemas lineares cujo número de equações é igual ao número de incógnitas e o determinante da matriz de coeficientes associada é diferente de zero, isto é, sistemas do tipo SPD.
Considere um sistema linear com três equações e três incógnitas:
E seja o determinante da matriz de coeficientes associados ao sistema linear. Então, se
, o sistema é SPD e podemos usar a Regra de Cramer.
1º passo) Calculamos e
, que são os determinantes obtidos substituindo a respectiva coluna da incógnita pelos termos independentes (
) das equações do sistema.
,
,
2º passo) Encontramos a solução do sistema, que é uma tripla ordenada (), onde:
Escalonamento
O escalonamento é um método que nos permite resolver sistemas lineares em que o número de equações pode ou não ser igual ao número de incógnitas. Isso significa que o sistema não precisa ser necessariamente SPD para usar esse método.
1º passo) Escrever a matriz associada com todos os coeficientes, inclusive os termos independentes;
2º passo) Realizar operações necessárias entre as linhas da matriz para obter uma matriz escalonada;
3º passo) Montar o sistema linear associado à matriz escalonada;
4º passo) Resolver o sistema, que será um sistema simples de obter as soluções, bastando isolar as incógnitas.
As operações que podem ser realizadas entre as linhas da matriz são:
- Trocar uma linha de lugar com outra;
- Somar ou subtrair uma linha por outra;
- Multiplicar ou dividir uma linha toda por um número diferente de zero.
Exemplo: Determine a solução do sistema linear .
Vamos utilizar o método do escalonamento para resolver o sistema.
1º passo) A matriz de coeficientes (completa) possui três linhas () e é dada por:
2º passo) Vamos realizar as operações entre as linhas até obter a matriz escalonada.
3º passo) O sistema linear associado à matriz escalonada é:
4º passo) Resolvemos o sistema:
Da última equação, temos que .
Substituindo na segunda equação, temos que
.
Substituindo e
na primeira equação, temos que
.
Portanto, a solução do sistema é a tripla ordenada .
Você também pode se interessar:

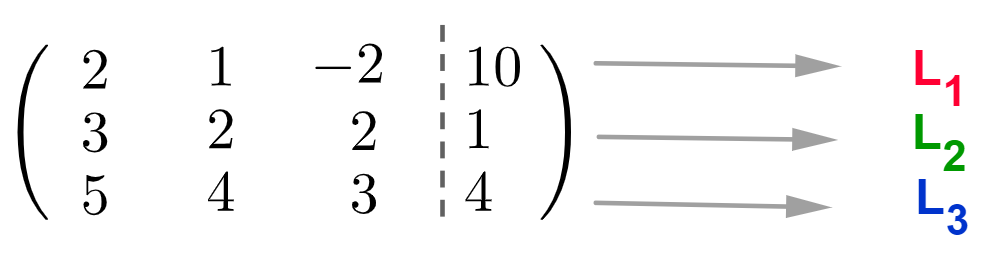

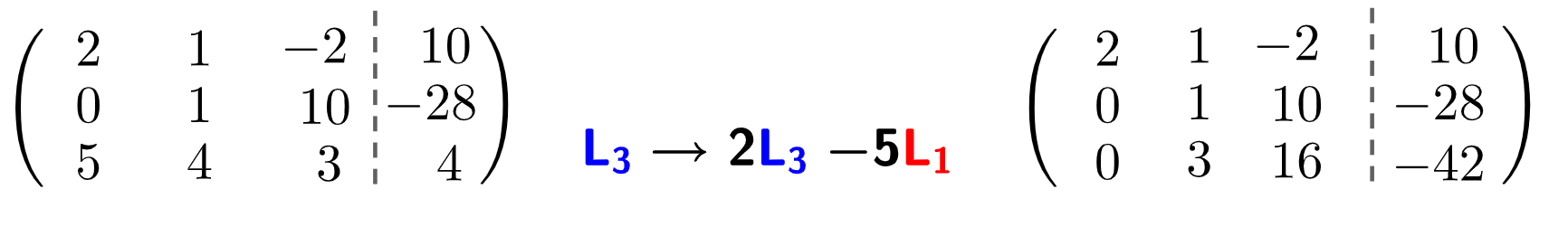

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.