Triângulo de Pascal
Triângulo de Pascal é um triângulo formado apenas por números, com propriedades matemáticas importantes e características que chamam a atenção.
Triângulo de Pascal é um triângulo formado apenas por números, com propriedades matemáticas importantes e características que chamam a atenção.
Os números das extremidades do triângulo de Pascal são todos iguais a 1 e cada um dos demais números corresponde a soma dos dois números que estão acima.
Na figura, é apresentada apenas uma parte do triângulo de Pascal, mas podem ser construídas infinitas linhas de números logo abaixo, pois ele é infinito.
História do triângulo de Pascal
O nome Triângulo de Pascal se deve ao filósofo, físico e matemático francês Blaise Pascal (1623 – 1662), por ter escrito sobre ele em Traité du triangle arithmétique (1654).
Muitas vezes, esse triângulo também é chamado de triângulo de Tartaglia, em menção ao matemático italiano Tartaglia (1500 – 1557), por ter sido um dos primeiros a publicar sobre o triângulo na Europa.
Contudo, o triângulo já era conhecido e suas propriedades eram estudadas por outros matemáticos indianos e chineses tempos antes de Tartaglia e Pascal.
Coeficiente binomial e o triângulo de Pascal
Um coeficiente binomial ou número combinatório possui a seguinte forma:
Em que e
são números naturais, com
, e
indica o número de grupos de tamanho
que podem ser formados com
elementos.
O símbolo de exclamação (!) indica fatorial, por exemplo, .
Mas o que isso tem a ver com o triângulo de Pascal? O triângulo de Pascal é construído a partir de coeficientes binomiais.
Cada um dos números que formam o triângulo de Pascal é um coeficiente binomial e pode ser obtido a partir dessa fórmula acima.
Construção do triângulo de Pascal
Para construção de cada linha triângulo de Pascal, consideramos os coeficientes binomiais com numerador (número de cima) igual ao número da linha e denominador (número de baixo) variando de zero até o número da linha.
Lembre-se: a primeira linha do triângulo é a linha de número 0 e não número 1.
Considere, por exemplo, construir a 3ª linha do triângulo, o numerador será sempre 3 e o denominador será 0, 1, 2, e 3, formando os seguintes coeficientes binomiais:
Então, calculamos cada uma dessas combinações e já temos os valores da 3ª linha do triângulo:
Portanto, a 3ª linha do triângulo de Pascal é formada pelos números:
1 3 3 1
Veja como fica o triângulo escrito em função dos coeficientes binominais:
Propriedades do triângulo de Pascal
Como pode ser observado no triângulo de Pascal, os números das extremidades são todos iguais a 1, então, toda linha começa com 1 e termina com 1.
Isso pode ser verificado a partir dos coeficientes binomiais. O primeiro elemento de uma linha é
e o último é
. Para qualquer que seja o valor de
, temos:
Essa propriedade também pode ser vista, facilmente, observando o triângulo. A partir dos coeficientes binomiais, ela pode ser constatada da seguinte forma:
Se o triângulo de Pascal for dividido ao meio, perceberemos que os números de uma parte serão os mesmos da outra, pois ele é simétrico.
As linhas do triângulo de Pascal são enumeradas, 0, 1, 2, 3, 4, 5, …, infinitamente.
Se escolhermos a linha 3, por exemplo, veja que a soma dos elementos é 1 + 3 + 3 + 1 = 8 e que .
Isso acontece em qualquer linha do triângulo, então, sem conhecer os elementos da linha 15, podemos dizer que a soma será igual a .
Binômio de Newton e o triângulo de Pascal
O binômio de Newton é uma fórmula que permite calcular potências de binômios da forma , com
sendo um número natural.
Se atribuirmos valores para e aplicarmos a fórmula, poderemos ver que os coeficientes binomiais são os mesmos números do triângulo de Pascal:
Triângulo de Sierpinski e o triângulo de Pascal
Quando os números pares e ímpares do triângulo de Pascal são diferenciados com cores, a figura obtida é muito semelhante ao Triângulo de Sierpinski, que é um tipo de fractal, uma figura geométrica com padrão de repetição infinito.
Você também pode se interessar:
- Probabilidade
- Sequência de Fibonacci
- Número de ouro
- Contribuições de René Descartes para a matemática



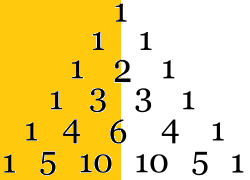


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.