Lista de exercícios de geometria analítica
Confira uma lista de exercícios de geometria analítica, todos com resolução. Questões de distância, ponto médio, equação da reta, coeficiente angular, e muito mais!
Geometria analítica é uma parte da matemática que estuda as figuras geométricas a partir de expressões algébricas e usando um sistema de coordenadas.
Veja a seguir uma lista de exercícios de geometria analítica, todos com resolução, para que você possa entender o tipo de questões desse ramo da matemática.
Lista de exercícios de geometria analítica
Questão 1. Determine as coordenadas do ponto médio do segmento de extremidades A(1,6) e B(5, 3).
Questão 2. Determine as coordenadas do ponto médio do segmento de extremidades A(-4,0) e B(7, -2).
Questão 3. O ponto M(1, -2) é o ponto médio do segmento de extremidades A() e B(-1, -5). Determine as coordenadas do ponto A.
Questão 4. Determine as coordenadas do baricentro de um triângulo de vértices A(1, 2), B(4, 4) e C(5, 1).
Questão 5. A distância entre os pontos A(1,8) e B(x, -2) é 2√29. Determine a abscissa do ponto B.
Questão 6. Verifique se os pontos A(2, 1), B(4, 2) e C(6, 3) são pontos alinhados.
Questão 7. Os pontos A(-8, y), B(-2, -1) e C(1, -3) são alinhados. Encontre a ordenada do ponto A.
Questão 8. Escreva a equação reduzida e geral da reta que passa pelos pontos A(1, 1) e B(-4, -2).
Questão 9. Determine a equação da reta que passa por A(2, 3) e é paralela à reta 2x + y = -2.
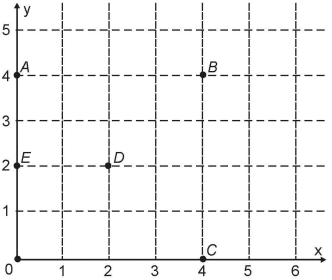
Questão 10. (Enem 2018) Um jogo pedagógico utiliza-se de uma interface algébrico-geométrica do seguinte modo: os alunos devem eliminar os pontos do plano cartesiano dando “tiros”, seguindo trajetórias que devem passar pelos pontos escolhidos. Para dar os tiros, o aluno deve escrever em uma janela do programa a equação cartesiana de uma reta ou de uma circunferência que passa pelos pontos e pela origem do sistema de coordenadas. Se o tiro for dado por meio da equação da circunferência, cada ponto diferente da origem que for atingido vale 2 pontos. Se o tiro for dado por meio da equação de uma reta, cada ponto diferente da origem que for atingido vale 1 ponto. Em uma situação de jogo, ainda restam os seguintes pontos para serem eliminados: A(0 ; 4), 6(4 ; 4), C(4 ; 0), D(2 ; 2) e E(0; 2).
Passando pelo ponto A, qual equação forneceria a maior pontuação?
A) x = 0
B) y = 0
C) x² + y² =16
D) x² + (y – 2)² = 4
E) (x – 2 )² + ( y – 2 )² = 8
Resolução da questão 1
Ponto médio :
Então, o ponto médio é o ponto .
Resolução da questão 2
Ponto médio :
Então, o ponto médio é o ponto .
Resolução da questão 3
Portanto, A(3, 1).
Resolução da questão 4
O baricentro (G) é o ponto de encontro das medianas do triângulo.
O baricentro é ponto .
Resolução da questão 5
Vamos usar a fórmula da distância entre dois pontos.
Cálculo do discriminante:
e
Portanto, a abscissa do ponto B é 5 ou -3.
Resolução da questão 6
Os três pontos são alinhados se:
Então, vamos calcular o determinante pela Regra de Sarrus e ver se satisfaz essa condição:
(4 + 6 + 12) – (12 + 6 + 4) = 0
Como o determinante é igual a 0, então, os três são alinhados.
Resolução da questão 7
Se os três pontos são alinhados, então:
Vamos resolver o determinante para encontrar o valor de y:
8 + y + 6 – (-1 + 24 – 2y) = 0
8 + y + 6 + 1 – 24 + 2y = 0
3y – 9 = 0
3y = 9
y = 3
Portanto, a ordenada do ponto A é y = 3.
Resolução da questão 8
Coeficiente linear, considerando o ponto (1,1) e o valor de m encontrado:
Equação geral da reta:
Resolução da questão 9
Retas paralelas têm o mesmo coeficiente angular, então, vamos determinar o coeficiente angular da reta 2x + y = -2, escrevendo-a na forma y = mx + n.
2x + y = -2
y = -2x – 2
Então, m = -2.
Agora, encontramos a equação da reta que passa por A(2, 3) e tem coeficiente angular m = -2.
y = mx + n
3 = -2 . 2 + n
n = 7
Equação reduzida da reta:
y = mx + n
y = -2x + 7
Equação geral da reta:
y = -2x + 7
2x + y – 7 = 0
Resolução da questão 10
Para resolver essa questão, vamos analisar cada uma das alternativas, observando os pontos pelos quais a reta ou circunferência passa e a pontuação.
Letra A: reta x = 0, que corresponde ao eixo y e passa pelos pontos A e E ⇒ pontuação: 1 + 1 = 2.
Letra B: reta y = 0, que corresponde ao eixo x e passa pelo ponto C ⇒ pontuação: 0.
Letra C: circunferência x² + y² =16, de centro C(0,0) e raio r = 4, passando pelos pontos A e C ⇒ pontuação: 2 + 2 = 4.
Letra D: circunferência x² + (y – 2)² = 4, de centro C(0, 2) e raio r = 2, passando pelos pontos A e D ⇒ pontuação: 2 + 2 = 4.
Letra E: circunferência (x – 2 )² + ( y – 2 )² = 8, de centro C(2, 2) e raio r = 2√2, passando pelos pontos A, B e C ⇒ pontuação: 2 + 2 + 2 = 6.
Alternativa correta: E.
Você também pode se interessar:
- Plano cartesiano
- Lista de exercícios de estatística
- Exercícios de probabilidade
- Exercícios de função do primeiro grau (função afim)
- Exercícios sobre função quadrática

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.