Tronco de pirâmide

O tronco de pirâmide é a parte inferior da pirâmide sem o seu vértice. Ele é obtido a partir de um corte feito por um plano paralelo à sua base.

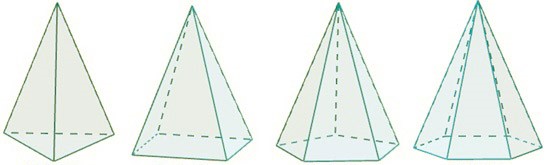
Lembre-se de que as pirâmides são sólidos geométricos e podem variar conforme sua base. Veja alguns tipos de pirâmides:

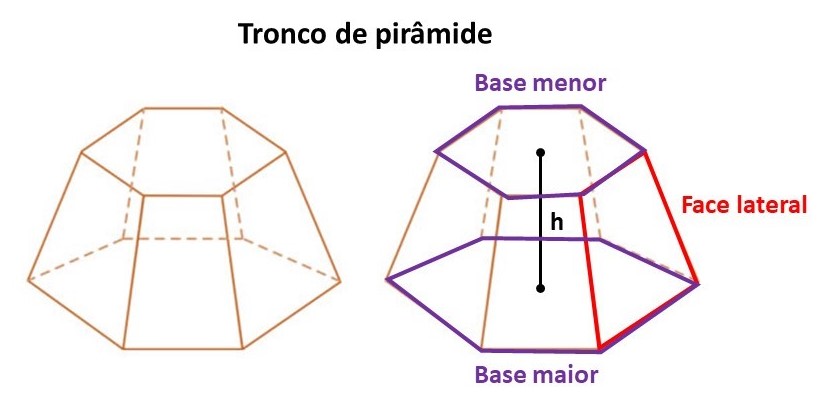
Para cada tipo de pirâmide, podemos obter um tronco de pirâmide com base diferente. Considere, por exemplo, o tronco de pirâmide de base pentagonal:

Observações:

• O tronco de pirâmide sempre tem duas bases poligonais semelhantes, uma maior e outra menor.
• As faces laterais são trapézios, variando apenas em quantidade (de acordo com a base).

Área do tronco de pirâmide

A área do tronco de pirâmide corresponde à medida da sua superfície, de forma que podemos obter a área das bases, a área lateral e a área total da figura.

Área total:

A área total () do tronco de pirâmide pode ser calculada pela seguinte fórmula:

Em que:

• : área lateral;
• : área da base maior;
• : área da base menor.

Área das bases:

As bases são polígonos e podem variar, podem ser triângulos, quadrados, retângulos, pentágonos, hexágonos, entre outros. Por isso, precisamos saber calcular a área de polígonos.

Área lateral:

As laterais são trapézios, então, precisamos saber calcular a área dos trapézios. Por fim, somamos as áreas de todas as faces laterais, obtendo a área lateral.

Volume do tronco de pirâmide

O volume do tronco de pirâmide corresponde ao espaço ocupado ou capacidade do tronco da pirâmide.

Uma fórmula para determinar o volume do cone da pirâmide () pode ser encontrada quando subtraímos o volume da pirâmide menor obtida quando geramos um tronco de pirâmide do volume da pirâmide completa.

Em que:

• : altura do tronco;
• : área da base maior;
• : área da base menor.

Você também pode se interessar:

• Tronco de cone
• Volume da esfera
• Volume do cilindro
• Volume do cubo