Lista de exercícios de trigonometria

Elaboramos uma lista de exercícios de trigonometria, todos com resolução. Confira e aprenda mais sobre esse assunto!

Por Elainy Marciano Publicado em 31/07/2020 - 21:10

Trigonometria é a parte da matemática que estuda as relações entre os ângulos e os lados dos triângulos.

São diversas fórmulas, relações, teoremas e tabelas que fazem parte dos estudos de trigonometria, o que costuma causar um pouco de confusão na hora de resolver exercícios.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Pensando nisso, elaboramos uma lista de exercícios de trigonometria, todos com resolução, para que você possa tirar suas dúvidas sobre esse assunto!

Lista de exercícios de trigonometria

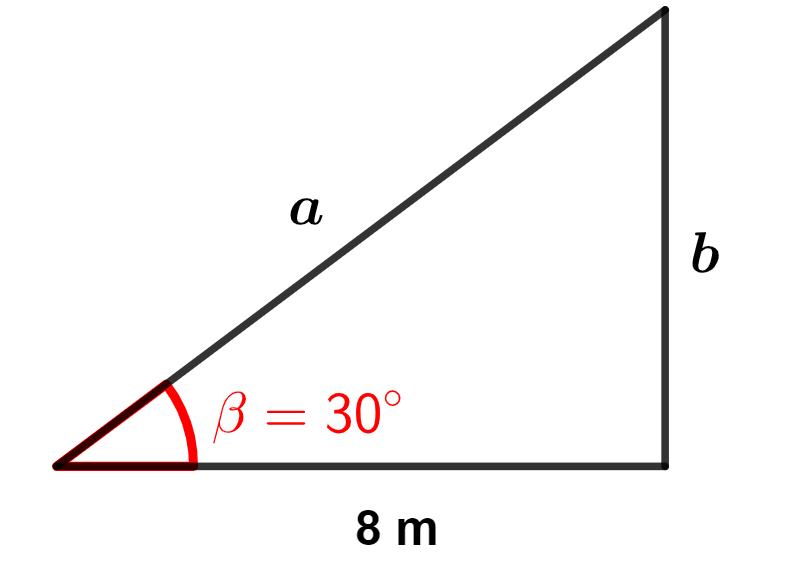
Questão 1. Calcule a altura de uma árvore, sabendo que se nos afastarmos 8 metros do tronco vemos o topo da árvore a partir de um ângulo de 30°.

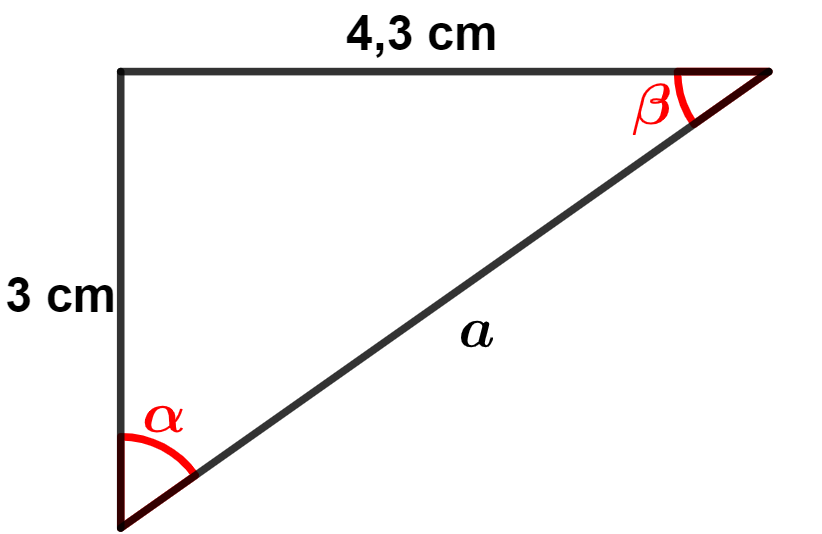
Questão 2. Determine a medida do lado $\dpi{120} a$ e as medidas dos ângulos $\dpi{120} \alpha$ e $\dpi{120} \beta$ no triângulo abaixo:

Questão 3. Calcule o valor do seno, cosseno e tangente do ângulo -120°.

Questão 4. Calcule o valor do seno, cosseno e tangente do ângulo 225°.

Questão 5. Mostre que, dado um ângulo $\dpi{120} \alpha$ , a soma da tangente e a cotangente é igual ao produto da secante e a cossecante: $\dpi{120} tan\: \alpha + cot \, \alpha = sec \, \alpha\cdot csc \, \alpha$

Resolução da questão 1

Pelas razões trigonométricas, temos que:

$\dpi{120} seno \, 30^{\circ}= \frac{cateto\, oposto}{hipotenusa} = \frac{b}{a}$

$\dpi{120} b = a\cdot seno \, 30^{\circ}$

Precisamos da hipotenusa ( $\dpi{120} a$ ) para descobrir o valor da altura $\dpi{120} b$ . Como sabemos o valor do cateto adjacente ao ângulo de 30°, vamos utilizar a seguinte razão:

$\dpi{120} cosseno \, 30^{\circ}= \frac{cateto\, adjacente}{hipotenusa} = \frac{8}{a}$

$\dpi{120} \Rightarrow a = \frac{8}{cosseno \, 30^{\circ}}$

A partir de uma tabela de ângulos notáveis ou em uma tabela trigonométrica, podemos verificar que cosseno de 30° é igual a $\dpi{120} \sqrt{3}/2$ . Assim:

$\dpi{120} a = \frac{8}{\frac{\sqrt{3}}{2}}$

$\dpi{120} \Rightarrow a = \frac{16}{\sqrt{3}} = 9, 23$

Agora que já sabemos o valor da hipotenusa, já podemos calcular a altura:

$\dpi{120} b = a\cdot seno \, 30^{\circ}$

$\dpi{120} \Rightarrow b = 9,23\cdot seno \, 30^{\circ}$

Seno de 30° é igual a $\dpi{120} 1/2$ , então:

$\dpi{120} \Rightarrow b = 9,23\cdot \frac{1}{2} = 4,61$

Portanto, a altura da árvore é igual a 4,61 metros.

Resolução da questão 2

Por se tratar de um triângulo retângulo e conhecermos a medida de dois lados, podemos utilizar o teorema de Pitágoras para determinar a medida do lado $\dpi{120} a$ , que corresponde a hipotenusa do triângulo.

$\dpi{120} a^2 = b^2 + c^2$

$\dpi{120} \Rightarrow a^2 = 3^2 + (4,3)^2$

$\dpi{120} \Rightarrow a^2 = 27,49$

$\dpi{120} \Rightarrow a = 5,24$

Agora, podemos encontrar as medidas dos ângulos utilizando as razões trigonométricas (pode ser o seno ou o cosseno):

$\dpi{120} seno \, \alpha= \frac{4,3}{5,24} \Rightarrow seno\, \alpha = 0,82\Rightarrow \alpha = seno^{-1}(0,82) = 55,08$

$\dpi{120} seno \, \beta= \frac{3}{5,24} \Rightarrow seno \, \beta=0,57\Rightarrow \beta = seno^{-1}(0,57) = 34,75$

Portanto, temos $\dpi{120} a = 5,24 cm$ , $\dpi{120} \alpha = 55,08^{\circ}$ e $\dpi{120} \beta = 34,75^{\circ}$ .

Resolução da questão 3

Temos que:

$\dpi{120} seno\: (-x) = -seno (x)$

$\dpi{120} cosseno\: (-x) = cosseno (x)$

$\dpi{120} tangente\: (-x) = -tangente (x)$

Considerando essas relações e o fato de que 120° = 180° – 60°, então:

$\dpi{120} seno\: (-120^{\circ}) = -seno (180^{\circ} - 60^{\circ})$

$\dpi{120} cosseno\: (-120^{\circ}) = cosseno (180^{\circ} - 60^{\circ})$

$\dpi{120} tangente\: (-120^{\circ}) = -tangente (180^{\circ} - 60^{\circ})$

Agora, utilizando as relações trigonométricas entre os valores das funções de ângulos suplementares e sabendo que seno 60° = $\dpi{120} \sqrt{3}/2$ ,cosseno 60° = 1/2 e tangente 60° = seno 60°/cosseno 60°, temos que:

$\dpi{120} seno\: (-120^{\circ}) = -seno (180^{\circ} - 60^{\circ}) = -seno (60^{\circ}) = -\sqrt{3}/2$

$\dpi{120} cosseno\: (-120^{\circ}) = cosseno (180^{\circ} - 60^{\circ}) = - cosseno (60^{\circ}) = -1/2$

$\dpi{120} tangente\: (-120^{\circ}) = -tangente (180^{\circ} - 60^{\circ}) = - tangente (60^{\circ}) = -\sqrt{3}$

Resolução da questão 4

Considerando o fato de que 225° = 180° + 45° e as relações vistas no exercício anterior, temos que:

$\dpi{120} seno\: (225^{\circ}) = seno (180^{\circ} + 45^{\circ}) = seno(-45^{\circ}) = -seno(45^{\circ})$

$\dpi{120} cosseno\: (225^{\circ}) = cosseno (180^{\circ} + 45^{\circ}) = -cosseno(-45^{\circ}) = -cosseno(45^{\circ})$

$\dpi{120} tangente\: (225^{\circ}) = tangente (180^{\circ} + 45^{\circ}) = -tangente(-45^{\circ}) = tangente(45^{\circ})$

Sabendo que seno 45° = cosseno 45° = $\dpi{120} \sqrt{2}/2$ e tangente 45° = seno 45°/cosseno 45°, temos que:

$\dpi{120} seno(225^{\circ}) = -\sqrt{2}/2$

$\dpi{120} cosseno(225^{\circ}) = -\sqrt{2}/2$

$\dpi{120} tangente(225^{\circ}) = 1$

Resolução da questão 5

Como $\dpi{120} tan \, \alpha = \frac{sen\, \alpha}{cos\, \alpha}$ e $\dpi{120} cot \, \alpha = \frac{cos\, \alpha}{sen\, \alpha}$ , então:

$\dpi{120} tan\: \alpha + cot \, \alpha = \frac{sen\, \alpha}{cos\, \alpha} + \frac{cos \, \alpha}{sen \, \alpha}$

Extraindo o MMC, temos que:

$\dpi{120} tan\: \alpha + cot \, \alpha = \frac{sen^2\, \alpha + cos^2\, \alpha }{cos\, \alpha \cdot sen\, \alpha }$

Considerando a relação fundamental $\dpi{120} sen^2 \, \alpha + cos^2 \, \alpha = 1$ , temos que:

$\dpi{120} tan\: \alpha + cot \, \alpha = \frac{1 }{cos\, \alpha \cdot sen\, \alpha }$

Como $\dpi{120} \frac{1}{cos\, \alpha\cdot sen\, \alpha} = \frac{1}{cos\, \alpha} \cdot \frac{1}{sen\, \alpha} = sec \, \alpha\cdot csc \, \alpha$ , então:

$\dpi{120} tan\: \alpha + cot \, \alpha = sec \, \alpha\cdot csc \, \alpha$

Você também pode se interessar: