Binômio de Newton
Conheça a importante fórmula matemática que leva o nome de Isaac Newton. Saiba para que serve e veja exemplos!
Binômio de Newton é uma fórmula que possibilita calcular uma potência de um binômio da forma , sendo o expoente
um número natural e
e
dois números reais quaisquer.
O binômio de Newton recebe esse nome em homenagem ao físico e matemático Isaac Newton, pois embora o binômio tenha surgido bem antes de sua época, os estudos de Newton foram mais abrangentes, envolvendo o caso de expoentes racionais.
A fórmula do binômio de Newton é:
Desenvolvendo esse somatório, temos que:
Em que:
É uma combinação de elementos tomados
a
. O símbolo de exclamação (!) indica um número fatorial.
Exemplo:
Pela fórmula do binômio de Newton, o binômio pode ser escrito da seguinte forma:
Agora, calculamos cada uma das combinações nessa soma:
Substituindo os resultados na expressão anterior, temos que:
Simplificando, chegamos na expressão final para o binômio:
Termo geral do binômio de Newton
O termo geral do binômio de Newton é uma fórmula que permite calcular o valor de um termo do binômio sem precisar desenvolver algebricamente todo o binômio, como fizemos no exemplo anterior.
A fórmula é:
Exemplo:
Vamos determinar o 7º termo do binômio usando a fórmula do termo geral.
Queremos obter , então,
.
E temos que .
Substituindo na fórmula, obtemos:
Como , então:
Simplificando:
Triângulo de Pascal
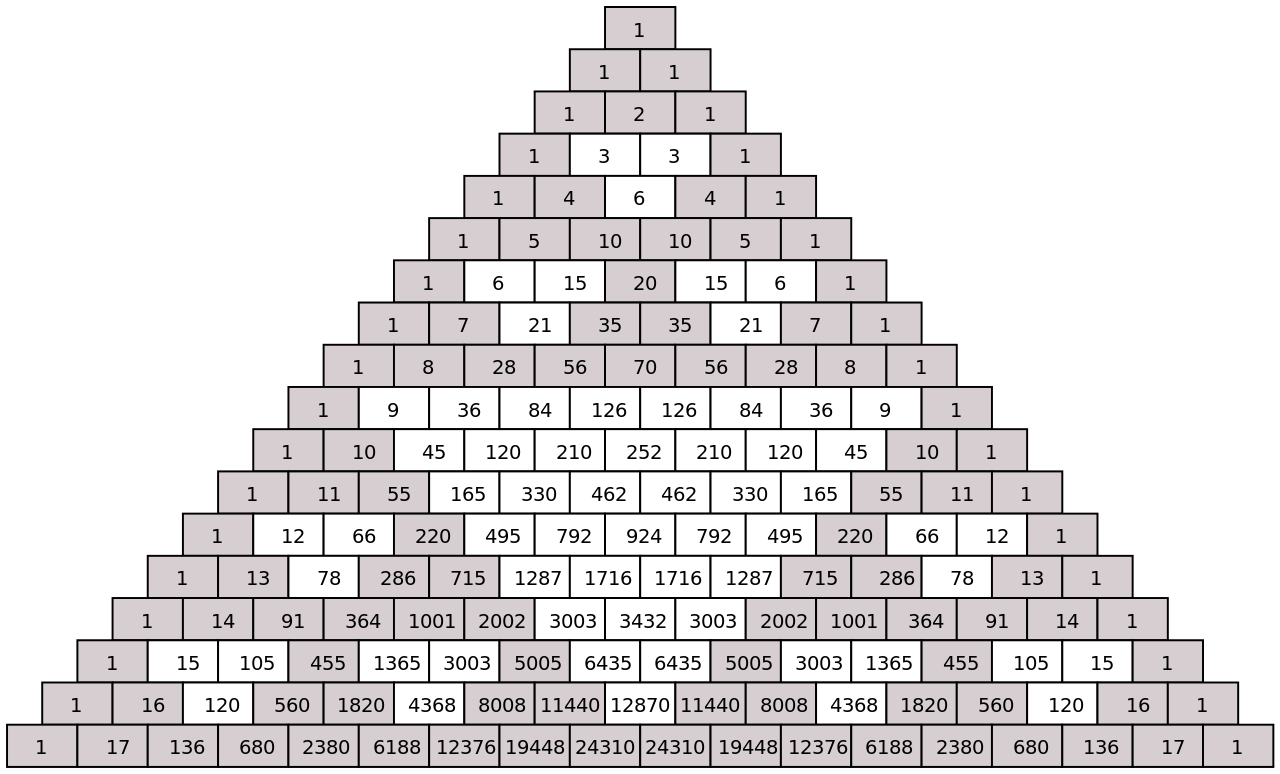
Triângulo de Pascal é um triângulo formado por números, cujos extremos são todos iguais a 1 e na parte interior, cada número é obtido como a soma dos dois números acima dele.
O triângulo de Pascal possui muitas propriedades e está relacionado ao binômio de Newton.
Cada fileira do triângulo de Pascal corresponde aos coeficientes obtidos com o desenvolvimento do binômio de Newton com potência igual ao número da fileira.
Você também pode se interessar:
- Lista de exercícios de números fatoriais
- Fatoração de polinômios
- Adição e subtração de polinômios
- Análise combinatória

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.