Lista de exercícios de área de figuras planas

O cálculo de áreas tem diversas aplicações, mas causa dúvidas em muitos estudantes. Em razão disso, preparamos uma lista com 10 exercícios resolvidos sobre área de figuras planas.

Por Elainy Marciano Publicado em 19/03/2020 - 11:48

Saber a área de uma figura geométrica plana significa saber a medida da superfície da figura, ou seja, o espaço ocupado por ela. Por isso, o cálculo de áreas tem diversas aplicações.

A seguir, temos uma lista com 10 exercícios resolvidos sobre área de figuras planas.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Lista de exercícios de área de figuras planas

Exercício 1
Calcule a área de um quadrado que possui perímetro igual a 24 cm.

Exercício 2

Calcule a área de um retângulo cuja base mede 1800 centímetros e a altura, 9 metros.

Exercício 3
Calcule a área de um canteiro de flores em formato de losango, que possui diagonal maior medindo 10 metros e diagonal menor medindo 5 metros.

Exercício 4
Qual é a área de um triângulo com base medindo 30 cm e altura igual a $\frac{2}{5}$ da medida da base?

Exercício 5
Com uma lata de tinta dá para pintar 10 m² de um muro. É necessário comprar quantas latas de tinta para pintar o muro todo sabendo que ele tem 20 metros de comprimento e 2,8 metros de altura?

Exercício 6
Em uma praça com formato circular, a distância do centro da praça até a extremidade da praça é de 15,7 metros. Qual a área total dessa praça?

Exercício 7
A planificação de uma caixa com 17 cm de comprimento, 5 cm de largura e 24 cm de altura é apresentada na figura abaixo. Qual a quantidade de papelão necessária para fazer uma caixa com essas dimensões?

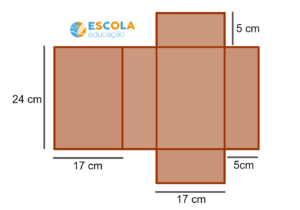
Exercício de área — Caixa de papelão planificada.

Exercício 8
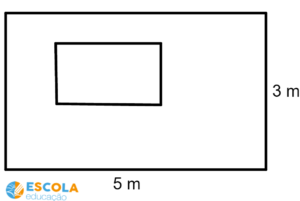
Quantos metros quadrados de azulejo são necessários para revestir uma parede com as dimensões apresentadas na figura abaixo e que possui uma janela que ocupa um espaço de 2 m²?

Exercício 9
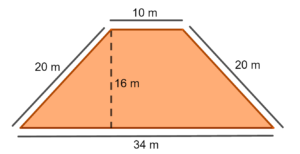
(Saresp) A figura mostra a planta de um terreno, com a indicação de algumas medidas. Qual a área desse terreno?

a) 84 m²

b) 160 m²

c) 300 m²

d) 352 m²

Exercício 10
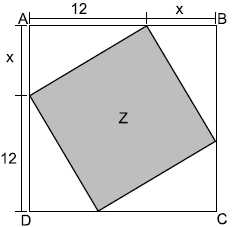
(TJ SP 2014 – Vunesp). Em uma folha quadrada ABCD, foi desenhado um quadrado Z, de área igual a 169 cm², conforme mostra a figura:

É correto afirmar que o perímetro da folha ABCD, em centímetros, é igual a:
a) 60
b) 56
c) 72
d) 68
e) 64

Resolução do exercício 1

O perímetro de um quadrado corresponde a soma das medidas dos lados do quadrado. Como todos os lados tem o mesmo tamanho, basta dividir o perímetro por 4 para saber a medida do lado.

$\dpi{120} \textnormal{lado do quadrado} = \frac{24 cm}{4}= 6 cm$

Assim, o lado desse quadrado mede 6 cm. Utilizando a fórmula da área de um quadrado, temos que:

$\dpi{120} A = (\textnormal{medida do lado})^2$

$\dpi{120} A = (6cm)^2$

$\dpi{120} A = 36cm^2$

Portanto, a área desse quadrado é igual a 36 cm².

Resolução do exercício 2

No cálculo de áreas, precisamos das medidas na mesma unidade. Nesse retângulo, a medida da base é dada em centímetros e a altura, em metros.

Desse modo, antes de calcular a área vamos transformar a medida da base para metros, dividindo por 100:

$\dpi{120} 1800 \div 100 = 18$

Logo, a medida da base é igual a 18 metros.

Utilizando a fórmula da área de um retângulo, temos que:

$\dpi{120} A= b\cdot h= 18 m \cdot 9 m= 162 m^2$

Assim, a área desse retângulo é igual a 162 m².

Resolução do exercício 3

A área de um losango é dada pelo produto das medidas das diagonais dividido por 2. Assim, nesse canteiro, a área é dada por:

$\dpi{120} A = \frac{D\cdot d}{2}= \frac{10m \cdot 5 m}{2}= \frac{50m^2}{2}= 25 m^2$

Ou seja, a área do canteiro é igual a 25 m².

Resolução do exercício 4

Para calcular a área de um triângulo, precisamos da medida da base ( $\dpi{120} b$ ) e da medida da altura ( $\dpi{120} h$ ).

Nesse exercício, temos $\dpi{120} b = 30 cm$ e $\dpi{120} h= \frac{2}{5}$ da medida da base.

Para saber o valor da altura, basta multiplicar a fração $\dpi{120} \frac{2}{5}$ pelo valor da base:

$\dpi{120} h=\frac{2}{5}\cdot 30cm=\frac{2\cdot 30cm}{5}=\frac{60cm}{5}=12cm$

Então, $\dpi{120} h=12cm$ . Assim, a área do triângulo é:

$\dpi{120} A=\frac{b\cdot h}{2}=\frac{30cm\cdot 12cm}{2}=\frac{360cm^2}{2}=180cm^2$

O triângulo tem 180 cm² de área.

Resolução do exercício 5

Para resolver esse exercício, precisamos calcular a área total do muro. Para isso, vamos utilizar a fórmula da área de um retângulo.

Temos base igual a 20 metros e altura igual a 2,8 metros, então:

$\dpi{120} A=b\cdot h=20m\cdot 2,8m=56m^2$

A área total do muro é igual a 56 m² e a cada 10 m² de muro será necessária uma nova lata de tinta.

Para saber o número de latas de tinta para pintar todo o muro, basta dividir a área do muro pela área que podemos pintar com uma lata, ou seja:

$\dpi{120} 56 m^2 \div 10 m^2=5,6$

Esse número significa que serão necessárias cinco latas completas e um pouco mais da metade de uma lata para pintar o muro. Assim, é necessário comprar 6 latas de tinta para pintar o muro todo.

Se ficou com dúvidas na multiplicação do número com vírgula, clique aqui para aprender como multiplicar números decimais.

Resolução do exercício 6

A praça tem o formato de um círculo, então, para saber a área da praça, basta calcular a área de um círculo. O raio ( $\dpi{120} r$ ) é dado pela distância do centro do círculo até a extremidade, então temos $\dpi{120} r=15,7m$ .

Assim,

$\dpi{120} A=\pi\cdot r^2=3,14\cdot (15,7 m)^2=773,9786m^2$

Logo, a praça tem aproximadamente 774 m² de área.

Resolução do exercício 7

Na planificação obtemos seis retângulos, basta calcular a área de cada um deles e somar para obter a área total da caixa.

Para os dois retângulos que têm base igual a 24 cm e altura igual a 17 cm:

$\dpi{120} A_1= 24 cm \cdot 17cm=408 cm^2$

Para os dois retângulos que têm base igual a 24 cm e altura igual a 5 cm:

$\dpi{120} A_2= 24 cm \cdot 5cm=120 cm^2$

Para os dois retângulos que têm base igual a 17 cm e altura igual a 5 cm:

$\dpi{120} A_3= 17 cm \cdot 5 cm=85 cm^2$

Assim, a área total é:

$\dpi{120} A_T=408cm^2+408cm^2+120cm^2+120cm^2+85cm^2+85cm^2$

$\dpi{120} A_T=1226 cm^2$

Então, são necessários 1226 cm² de papelão para fazer essa caixa.

Resolução do exercício 8

Nesse exercício, temos que calcular a área da parede e subtrair a área da janela, onde não serão colocados azulejos.

A área da parede, que é o retângulo maior é dada por:

$\dpi{120} A=5m\cdot 3m=15m^2$

A área da janela, que é o retângulo menor, já foi dada, é igual 2 m². Fazendo a subtração:

$\dpi{120} 15m^2-2m^2=13m^2$

Logo, são necessários 13 m² de azulejo para revestir essa parede.

Resolução do exercício 9

O terreno tem o formato de um trapézio, então para saber a área do terreno, basta calcular a área de um trapézio com as seguintes dimensões: base maior = 34 m, base menor = 10 m e altura = 16 m.

Assim,

$\dpi{120} A = \frac{(B+b)\cdot h}{2}=\frac{(34 m + 10 m)\cdot 16 m}{2}=\frac{44m\cdot 16m}{2}=\frac{704m^2}{2}=352 m^2$

Logo, a alternativa correta é a letra d.

Resolução do exercício 10

O perímetro é dado pela soma dos lados do quadrado. Então, precisamos saber a medida do lado do quadrado ABCD. Como essa medida depende do valor x, a primeira coisa a fazer é determinar o valor de x.

Observe que x é a medida de um dos catetos de um triângulo retângulo com hipotenusa igual ao lado do quadrado Z e outro cateto medindo 12 cm. Então, se soubermos a medida do lado do quadrado Z, podemos utilizar o Teorema de Pitágoras para encontrar o valor de x.

Para determinar a medida do lado do quadrado Z, vamos utilizar a informação da área que foi dada:

A = 169 cm²

Pela fórmula da área de um quadrado, temos que:

$\dpi{120} A = (\textnormal{medida do lado})^2$

Depois de extrair a raiz quadrada nos dois lados da equação, temos que a medida do lado é dada por: $\dpi{120} \mathrm{medida\: do\: lado = \: } \sqrt{A}$