Lista de exercícios sobre planificação de sólidos geométricos

Confira uma lista de exercícios resolvidos e tire suas dúvidas sobre planificação de sólidos geométricos (figuras espaciais).

Por Elainy Marciano Publicado em 03/11/2020 - 18:19

A planificação de sólidos geométricos permite visualizar as figuras geométricas planas que formam suas superfícies. Dessa forma, podemos obter a área total da superfície do sólido geométrico.

A seguir, veja uma lista de exercícios sobre planificação de sólidos geométricos, todos com a resolução completa, para que você possa tirar suas dúvidas e aprender mais!

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Exercícios sobre planificação de sólidos geométricos

Questão 1. Mostre que a área total do cubo de aresta a é dada por:

$\dpi{120} \mathrm{A_t = 6a^2}$

Questão 2. Calcule a área de um cubo cuja aresta mede 10 cm.

Questão 3. Mostre que a área total do paralelepípedo retângulo de comprimento a, largura b e altura c, é dada por:

$\dpi{120} \mathrm{A_t = 2\cdot(ab + ac + bc)}$

Questão 4. Calcule a área total de um paralelepípedo retângulo de dimensões 8 m, 6 m e 1,5 m.

Questão 5. Mostre que a área total de um cilindro de altura h e raio da base igual a r, é dada por:

$\dpi{120} \mathrm{A_t=2\pi r\cdot (r +h)}$

Questão 6. Determine a área total de cilindro de altura 15 cm e raio da base igual a 6 cm.

Questão 7. Mostre que a área total de um cone de geratriz g e raio da base igual a r é dada por:

$\dpi{120} \mathrm{A_t = \pi r\cdot (r+g)}$

Questão 8. Calcule a área total de um cone cuja geratriz mede 9 cm e o raio da base é igual a 4 cm.

Resolução da questão 1

A área total do cubo é dada pela soma das áreas das suas faces.

No total, o cubo tem 6 faces e cada face é um quadrado de lado igual à medida da aresta. Assim, para obter a área total do cubo, basta calcular a área de um só desses quadrados e multiplicar por 6, que é o total de faces.

$\dpi{120} \mathrm{A_t = 6\cdot A_{Quadrado}}$

A área do quadrado de lado a (medida da aresta) é dada por:

$\dpi{120} \mathrm{A_{Quadrado} = a^2}$

Portanto, a área total do cubo é dada por:

$\dpi{120} \mathrm{A_t = 6a^2}$

Resolução da questão 2

Temos a = 10 cm. Vamos substituir esse valor na fórmula da área total do cubo:

$\dpi{120} \mathrm{A_t = 6a^2 = 6\cdot 10^2 = 6\cdot 100 = 600}$

Portanto, a área total do cubo é igual a 600 cm².

Resolução da questão 3

A área total do paralelepípedo retângulo é dada pela soma das áreas de suas faces.

No total, o paralelepípedo retângulo tem 6 faces, e todas elas são retângulos cujas medidas dependem das dimensões do paralelepípedo.

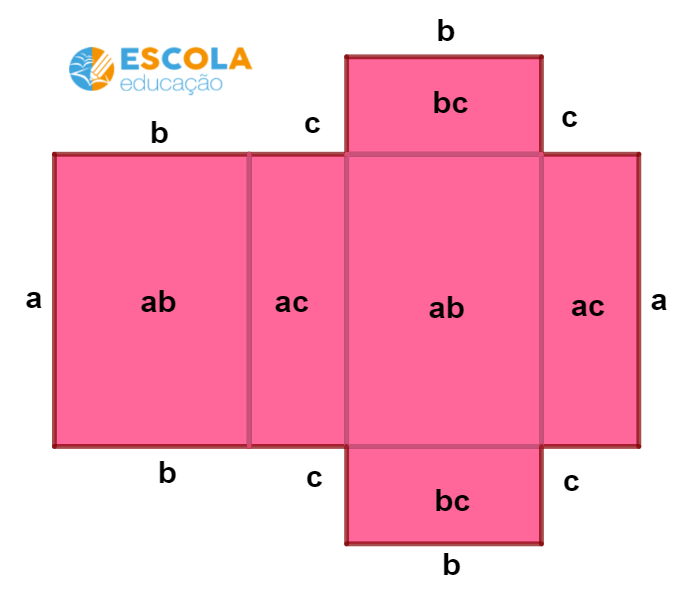
A partir da planificação, podemos ter uma ideia melhor das faces dessa figura geométrica:

A área de um retângulo qualquer é dada pela seguinte fórmula:

$\dpi{120} \mathrm{A_{Ret\hat{a}ngulo} = base\cdot altura}$

Assim, no paralelepípedo, temos dois retângulos de área ab, dois retângulos de área bc e dois retângulos de área ac, conforme pode ser visto na figura.

Portanto, a área total do paralelepípedo retângulo é:

$\dpi{120} \mathrm{A_t = 2ab + 2ac + 2bc}$

$\dpi{120} \Rightarrow \mathrm{A_t = 2\cdot(ab + ac + bc)}$

Resolução da questão 4

Temos a = 8 m, b = 6 m e c = 1,5 m. Vamos substituir esses valores na fórmula da área total do paralelepípedo retângulo:

$\dpi{120} \mathrm{A_t = 2\cdot(ab + ac + bc)}$

$\dpi{120} \Rightarrow \mathrm{A_t = 2\cdot(8.6 + 8.1,5 + 6.1,5)}$

$\dpi{120} \Rightarrow \mathrm{A_t = 2\cdot(48 + 12 + 9)}$

$\dpi{120} \Rightarrow \mathrm{A_t = 2\cdot69}$

$\dpi{120} \Rightarrow \mathrm{A_t = 138}$

Portanto, a área total do paralelepípedo é igual a 138 m².

Resolução da questão 5

Para calcular a área do total do cilindro, precisamos saber quais são as figuras planas que o formam, pois a sua área total será dada pela soma das áreas de cada uma dessas figuras.

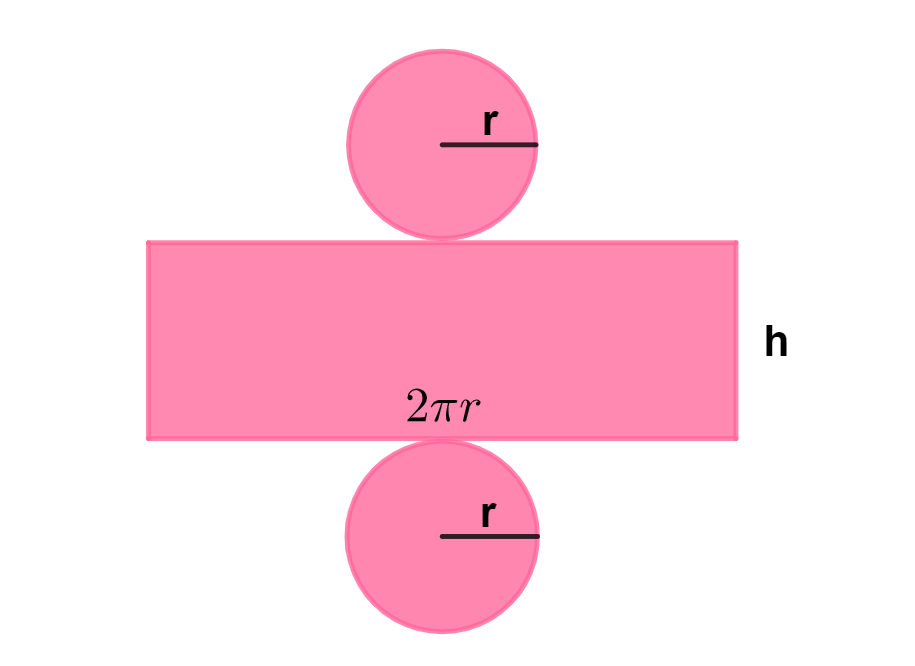
A partir da planificação do cilindro, podemos ver que ele é formado por três figuras geométricas planas: dois círculos e um paralelogramo.

Então, a área total do cilindro é dada por:

$\dpi{120} \mathrm{A_t = 2\cdot A_{Circulo} + A_{Paralelogramo}}$

A área do círculo é dada por:

$\dpi{120} \mathrm{A_{Circulo} = \pi r^2}$

E a área do paralelogramo é dada por:

$\dpi{120} \mathrm{A_{paralelogramo} = base\cdot altura = 2 \pi r\cdot h}$

No círculo de raio r, o comprimento é dado por 2πr, por isso, a medida da base do paralelogramo é 2πr, como pode ser visto na figura.

Então, a área total do cilindro é dada por:

$\dpi{120} \mathrm{A_t = 2\pi r^2 +2 \pi rh}$

$\dpi{120} \Rightarrow \mathrm{A_t = 2\pi r\cdot (r + h)}$

Resolução da questão 6

Temos h = 15 cm e r = 6 cm. Vamos substituir esses valores na fórmula da área total do cilindro:

$\dpi{120} \mathrm{A_t = 2\pi r\cdot (r + h)}$

$\dpi{120} \Rightarrow \mathrm{A_t = 2\pi 6\cdot (6 + 15)}$

$\dpi{120} \Rightarrow \mathrm{A_t = 252\pi }$

Considerando π = 3.14, a área do total do cilindro é igual a 791,28 cm².

Resolução da questão 7

Para calcular a área total do cone, devemos saber quais as figuras planas que o formam. A área total será dada pela soma das áreas de cada uma dessas figuras.

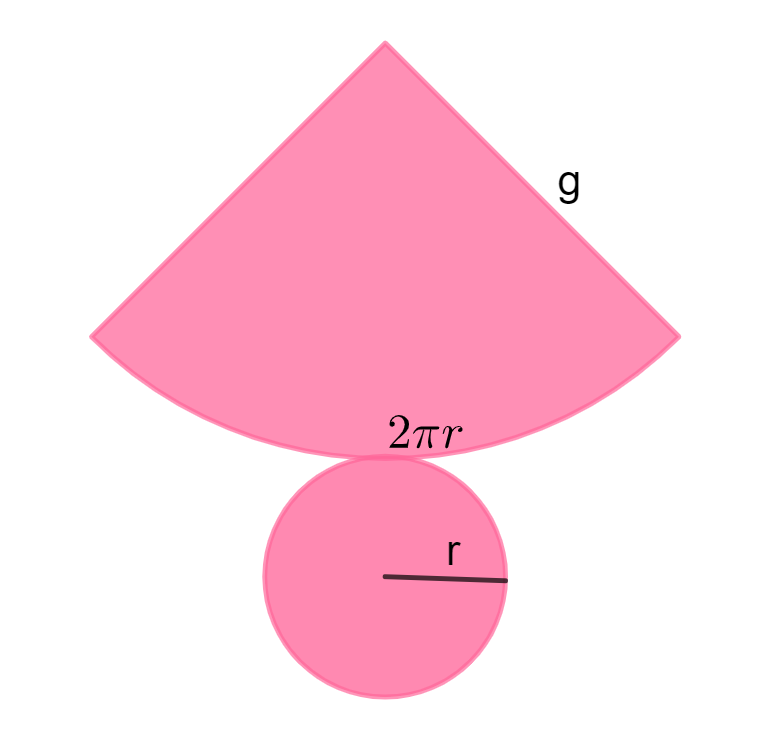
A partir da planificação do cone, podemos ver que ele é formado por um setor circular e um círculo.