Plano de aula – Teorema de Tales – 9º ano do Ensino Fundamental
Confira um plano de aula sobre o teorema de Tales em conformidade com a habilidade EF09MA12 da Base Nacional Comum Curricular (BNCC).
O teorema de Talles é um dos mais importantes da matemática, permitindo resolver diversos problemas geométricos envolvendo triângulos e retas paralelas cortadas por transversais.
O teorema é atribuído a Tales de Mileto, filósofo, matemático e astrônomo da Grécia Antiga, que viveu por volta de 600 anos antes de Cristo. Tales teria utilizado relações de proporcionalidade em triângulos para medir a altura da famosa pirâmide Quéops.
Veja, a seguir, uma sugestão de plano de aula sobre teorema de Tales, elaborado para o 9º ano do ensino fundamental, em conformidade com a habilidade EF09MA12 da Base Nacional Comum Curricular (BNCC).
Plano de aula – Teorema de Tales
TEMA: Teorema de Tales e relações de proporcionalidade.
HABILIDADES DA BNCC:(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
TEMPO SUGERIDO: 2 horas e 30 minutos (3 aulas de 50 minutos)
OBJETIVOS:
- Compreender a relação entre semelhança de triângulos e teorema de Tales;
- Utilizar o teorema de Tales para resolver problemas geométricos.
MATERIAL NECESSÁRIO:
- Lousa ou quadro negro;
- Pincel de cores variadas ou giz.
DESENVOLVIMENTO:
1º momento
Para compreender os conceitos dessa aula, o alunos precisam ter aprendido sobre razão e proporção, tipos de retas e semelhança de triângulos.
Inicie a aula perguntando como eles fariam para medir a altura de uma grande árvore, de um prédio ou de um poste de energia.
Deixe que eles debatam e proponham suas ideias sobre isso. Em seguida, explique como o matemático Tales de Mileto fez para medir uma enorme pirâmide usando seus conhecimentos sobre proporcionalidade, por volta de 600 anos a. C.
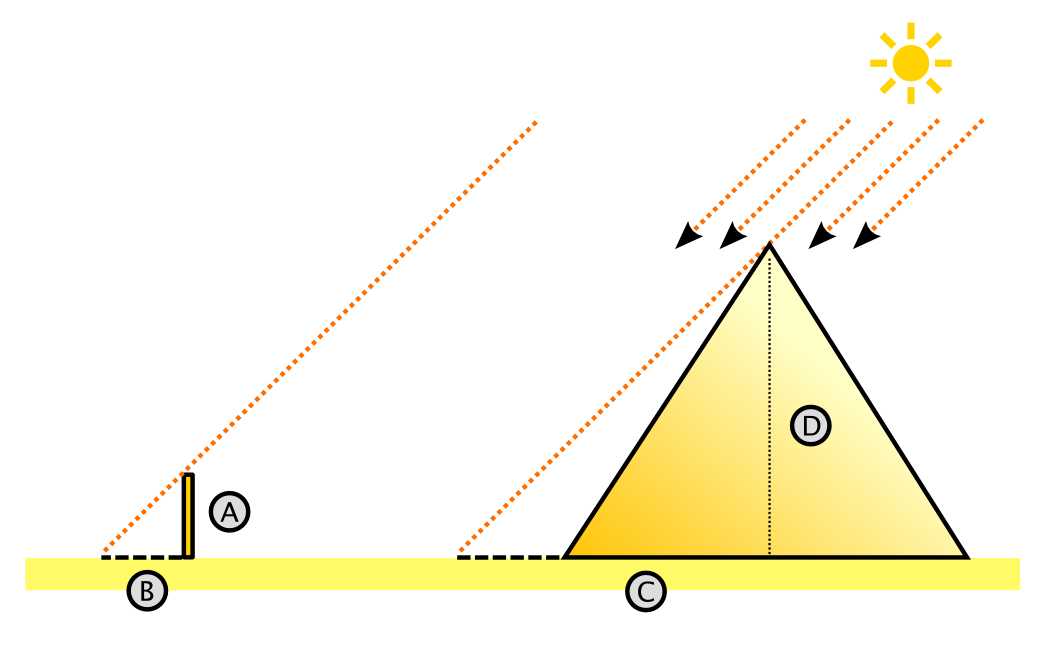
Enfatize o contexto da época, explique que Tales dispunha de objetos de medição simples, sem nenhum tipo de tecnologia e esquematize na lousa a figura a seguir.
Mostre qual foi a percepção que o matemático teve em relação aos triângulos formados a partir de um objeto fincado no solo, a pirâmide, suas respectivas sombras e os raios solares.
Explique que os raios solares são paralelos e que por isso os triângulos possuem ângulos de mesma medida, sendo um deles um ângulo reto (90°). Então, pela semelhança de triângulos, os lados correspondentes são proporcionais.
Atribua valores para A, B e C na figura e comente que essas medidas Tales conhecia, pois se referiam a altura do objeto, a medida da sua sombra no solo e a medida da sombra da pirâmide (somada a metade da medida da base da pirâmide). Peça para que calculem D, com base nos valores que você estipulou.
2º momento
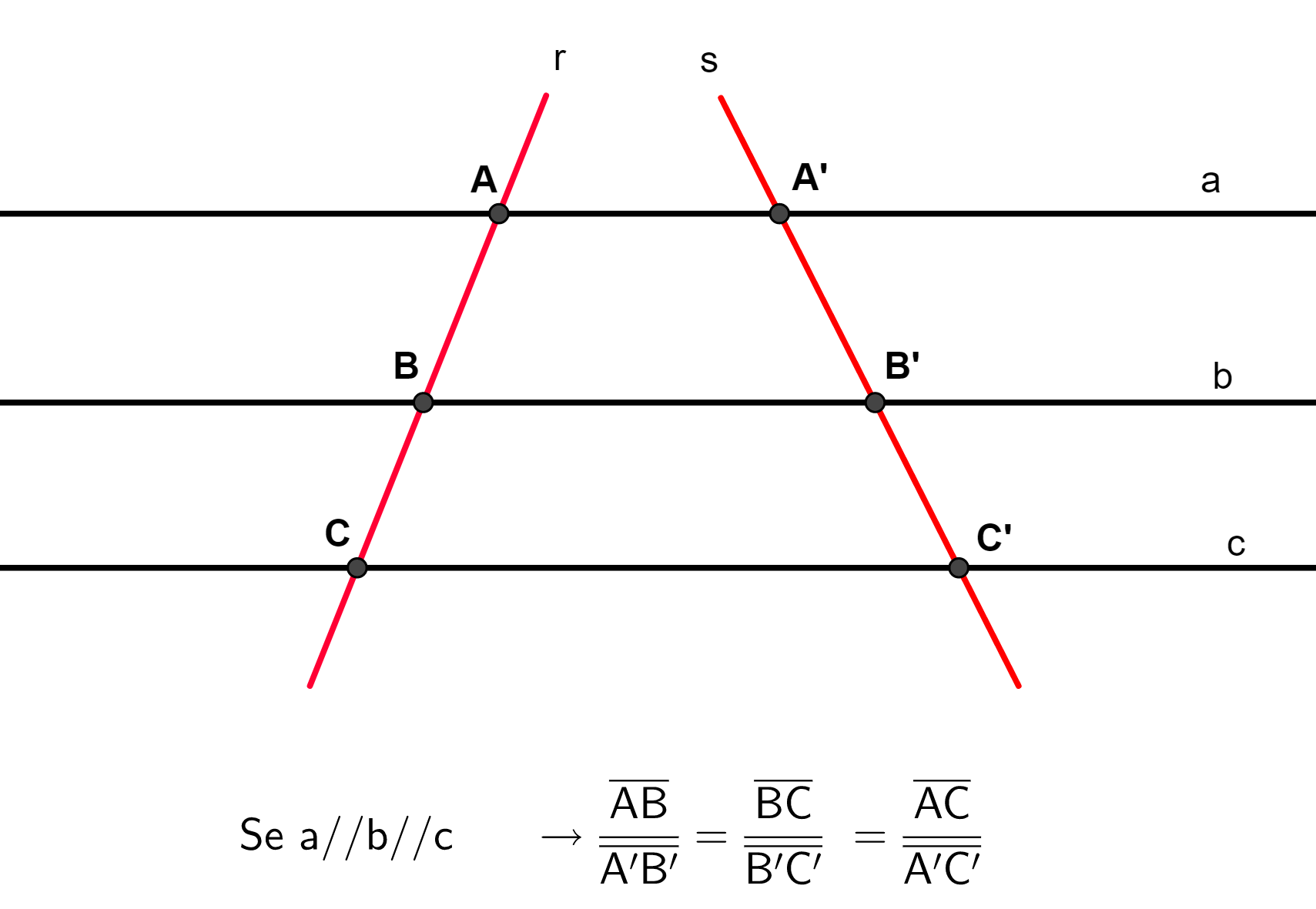
Enuncie o teorema de Tales na lousa e peça para anotarem em seus cadernos.
Explique que o número obtido em cada quociente é o mesmo e é chamado de razão de proporcionalidade.
Faça exemplos simples na lousa para mostrar como usar o teorema e proponha exercícios sobre o teorema de Talles.
AVALIAÇÃO:
A avaliação poderá ser feita a partir da observação dos alunos durante a aula, tanto na explicação dos conceitos quanto na realização das atividades.
Veja se eles entendem a relação entre semelhança de triângulos e o teorema de Tales e como eles o utilizam para resolver os exercícios propostos.
Para baixar o plano de aula sobre o Teorema de Tales em PDF, clique aqui!
Você também pode se interessar:
- Lista de exercícios sobre semelhança de triângulos
- Plano de aula de Matemática – Teorema de Pitágoras
- Plano de aula – Proporcionalidade dos triângulos – 9º ano do Ensino Fundamental
- Plano de aula – Bissetriz e mediatriz – 8º ano do Ensino Fundamental
- Plano de aula – Polígonos regulares – 8º ano do Ensino Fundamental
- Plano de aula – Propriedades dos quadriláteros – 8º ano do Ensino Fundamental

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.