Matemática no Enem
Saiba quais são os assuntos de matemática mais cobrados e veja dicas de como estudar e como fazer a prova do Enem para se dar bem!
O Exame Nacional do Ensino Médio (Enem) é dividido por áreas do conhecimento e 45 questões são de Matemática e suas tecnologias, que costumam causar terror nos candidatos.
Muitos estudantes trazem consigo uma relação traumática com a Matemática e se sentem perdidos na hora de se preparar para a prova.
O que falta, muitas vezes, é uma direção, um ponto de partida para que os estudos comecem a fluir normalmente e deixem de ser esse pesadelo que muitos consideram.
Pensando nisso, preparamos esse artigo com os assuntos mais cobrados no Enem, para que você possa saber em que deve se dedicar mais. Além disso, trazemos algumas dicas e sugestões para antes da prova e para o grande dia.
Confira nossas dicas para se dar bem em Matemática no Enem!
Assuntos que mais caem no Enem
A prova de Matemática do Enem abrange conteúdos diversificados e não é possível dizer com toda certeza quais serão os assuntos cobrados.
Contudo, a partir de provas anteriores, pode-se verificar que alguns assuntos são abordados com mais frequência na prova.
A seguir, listamos os assuntos de Matemática que mais caem no Enem.
Gráficos
Saber interpretar gráficos é primordial para se dar bem no Enem. Na prova, costumam ter várias questões com gráficos, pois eles podem estar associados a qualquer assunto de Matemática.
Estude vários tipos de gráficos, como o gráfico de barras, o gráfico de setores, o diagrama de dispersão, o gráfico de linhas, entre outros. É preciso saber extrair as informações dos gráficos!
Para saber mais, leia: Lista de exercícios de gráficos.
Razões e proporções
Para resolver muitas questões do Enem, você precisará dominar os conceitos de razão e proporção e a propriedade fundamental das proporções.
As razões são quocientes entre dois números e as proporções são igualdades entre duas razões.
Esses dois conceitos são amplamente usados em situações que envolvem relações entre grandezas, como tempo, distância, peso, altura ou qualquer outra coisa que possa ser medida.
Nesse sentido, é importante saber o que são grandezas diretamente e inversamente proporcionais.
Para saber mais, veja: Exercícios sobre razão e proporção.
Regra de três
Associada às temáticas anteriores, de razões, proporções e grandezas, podemos citar a regra de três como um assunto que também costuma cair na prova do Enem.
Regra de três é um procedimento que permite determinar um valor desconhecido em problemas que envolvem duas ou mais grandezas.
Para saber mais, veja: Exercícios de regra de três.
Probabilidade
Questões de probabilidade são muito comuns no Enem, então, não deixe de ir fazer a prova sem saber os principais conceitos e fórmulas de probabilidade.
Probabilidade é um ramo da Matemática que estuda a ocorrência de eventos aleatórios.
Além de saber como calcular a probabilidade de um único evento ocorrer, é importante saber, também:
- a probabilidade de somente um de dois eventos ocorrer (probabilidade da união);
- a probabilidade de dois eventos ocorrerem ao mesmo tempo, sejam eles independentes ou não (probabilidade da intersecção);
- a probabilidade de um evento ocorrer sabendo que outro evento já ocorreu (probabilidade condicional).
Para saber mais, veja: Exercícios de probabilidade.
Porcentagem
Porcentagem é um conteúdo básico e simples, mas muita gente ainda fica em dúvida quando elas aparecem.
Em qualquer outro assunto da prova de Matemática, pode ser necessário lidar com porcentagens. Assim, é de extrema importância aprender a trabalhar com elas e, consequentemente, com frações e números decimais.
Porcentagens são frações de denominador igual a 100, elas são usadas para indicar a participação de uma parte em relação ao todo. Qualquer porcentagem pode ser escrita na forma decimal, então, saiba como fazer essa transformação.
Para saber mais, veja: Exercícios de porcentagem.
Função afim e função quadrática
Diversas funções podem ser abordadas no Enem, mas as mais comuns são: função afim e função quadrática.
Função afim tem como gráfico uma reta e função quadrática, uma parábola. Então, você precisa saber interpretar esses gráficos.
Fique atento às características dessas funções e aos pontos notáveis, como os pontos de intersecção com os eixos, os zeros da função, entre outros.
Nas funções quadráticas, também chamadas de funções do 2º grau, as raízes podem ser determinadas pela famosa fórmula de Bhaskara ou pela soma e produto.
Para saber mais, leia:
Média, moda e mediana
Média, moda e mediana são três medidas de centralidade de um conjunto de dados, elas são usadas para resumir uma porção de valores através de um número.
Muitas questões envolvem esses três medidas de estatística. Por isso, saiba o que são, como se calcula, como interpretar e quais as particularidades de cada uma.
Pode ser que os dados sejam apresentados em uma tabela de frequência, o que facilita o cálculo dessas medidas. Mas, de nada adiantará se você não souber como lidar com esse tipo de tabela. Atente-se a isso!
Para saber mais, leia:
Área e volume de figuras geométricas
Quando se fala em Geometria Plana e Geometria Espacial, a área e o volume são, normalmente, as primeiras coisas que vêm à mente.
Pois saiba que no Enem sempre vai cair uma questão que envolva área e volume de figuras geométricas.
Então, para começar, é preciso estar claro que área é uma medida de figuras planas e volume é uma medida de figuras espaciais, aquelas em três dimensões.
A área de qualquer paralelogramo é dada pela base vezes altura, o que inclui quadrados e retângulos. Triângulos e trapézios são metade de um paralelogramo, por isso, nas fórmulas aparece a divisão por 2.
No caso da área dos triângulos, procure saber como calcular a altura utilizando apenas as medidas do lados, seja para triângulo equilátero, triângulo isósceles ou triângulo escaleno.
Em relação ao volume, você precisará saber a altura e a área da base, então, novamente, procure saber calcular área de figuras planas.
Para saber mais, leia:
Como estudar para o Enem
Cada pessoa tem sua própria maneira de estudar e suas estratégias de aprendizado. No entanto, preparamos algumas dicas e sugestões que podem ser muito úteis caso essa jornada ainda esteja meio confusa.
De um modo geral, no Enem ou qualquer outro exame, é fundamental que o estudante mantenha uma rotina de estudos, estabeleça horários e tenha organizado os conteúdos que precisa estudar.
Dito isso, vamos para algumas dicas e sugestões para você se preparar para a prova de Matemática do Enem.
1) Faça resumos, formulários ou mapas mentais dos conteúdos. Não dá para estudar Matemática apenas fazendo a leitura, estude sempre com uma folha do lado e faça anotações.
2) Resolva as questões das provas anteriores. Comece por aquelas mais simples, mas não desista das questões que você julga difíceis, procure resoluções das provas.
3) Abandone a calculadora. Durante a prova você não terá uma calculadora, então, aprenda e treine fazer todas as contas sem essa ferramenta.
4) Use aproximações em seus cálculos sempre que puder. A prova do Enem é uma prova extensa e você precisa criar estratégias para resolver as questões com agilidade, e essa é uma delas.
5) Não desista dos seus estudos. Se algo lhe parecer muito difícil e estressante, tente estudar outra coisa. Em outro momento, com tranquilidade, volte naquele conteúdo e tente compreendê-lo novamente.
Além dessas dicas, devemos lembrar que Matemática não é só cálculos, é interpretação de texto. Nas questões do Enem, há muita contextualização e você precisará interpretar para extrair as informações necessárias.
Questões de Matemática no Enem
As questões de Matemática do Enem costumam ser apresentadas com alguns textos nada curtos e para não perder informações importantes, faça a leitura sublinhando partes com números e grandezas, por exemplo.

Outras dica útil: pule questões da prova! Não corra o risco de não conseguir chegar ao final da prova e deixar de responder questões muito simples que estejam nas últimas páginas.
Então, se após ler uma questão, compreender o que deve ser feito e lhe parecer que sejam muitos cálculos, que demanda bastante tempo, deixe-a para responder depois.
Veja, a seguir, algumas questões do Enem resolvidas, para que você possa assimilar melhor sobre o tipo de questões de Matemática da prova.
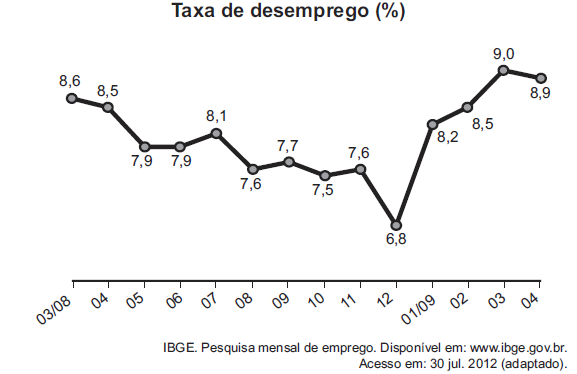
(Questão do Enem – 2017) O gráfico apresenta a taxa de desemprego (em %) para o período de março de 2008 a abril de 2009, obtida com base nos dados observados nas regiões metropolitanas de Recife, Salvador, Belo Horizonte, Rio de Janeiro, São Paulo e Porto Alegre.
A mediana dessa taxa de desemprego, no período de março de 2008 a abril de 2009, foi de
A) 8,1%
B) 8,0%
C) 7,9%
D) 7,7%
E) 7,6%
Questão resolvida e comentada:
A questão envolve um gráfico de linhas, porcentagens e cálculo da mediana. É uma questão simples de ser resolvida e que não demanda muito tempo.
O que deve ser observado é que as taxas apresentadas no gráfico não estão ordenadas (crescente ou decrescente), então, nada de determinar a mediana olhando apenas para o gráfico.
Para resolver, primeiro, ordenamos os dados:
6,8 7,5 7,6 7,6 7,7 7,9 7,9 8,1 8,2 8,5 8,5 8,6 8,9 9,0
Ao todo, são 14 valores, então, vamos calcular a mediana para um conjunto de dados com número par de observações.
Nesse caso, a mediana é a média das duas observações centrais (7ª e 8ª):
6,8 7,5 7,6 7,6 7,7 7,9 7,9 8,1 8,2 8,5 8,5 8,6 8,9 9,0
Portanto, a mediana das taxas de desemprego é 8,0%.
Alternativa correta: B.
(Questão do Enem – 2016) Um clube tem um campo de futebol com área total de 8000 m², correspondente ao gramado. Usualmente, a poda da grama desse campo é feita por duas máquinas do clube próprias para o serviço. Trabalhando no mesmo ritmo, as duas máquinas podam juntas 200 m² por hora. Por motivo de urgência na realização de uma partida de futebol, o administrador do campo precisará solicitar ao clube vizinho máquinas iguais às suas para fazer o serviço de poda em um tempo máximo de 5 h.
Utilizando as duas máquinas que o clube já possui, qual o número mínimo de máquinas que o administrador do campo deverá solicitar ao clube vizinho?
A) 4
B) 6
C) 8
D) 14
E) 16
Questão resolvida e comentada:
Essa é uma questão que envolve três grandezas: área, tempo e número de máquinas, e pode ser resolvida a partir da interpretação e alguns cálculos simples.
Se duas máquinas podam juntas 200 m² por hora, no mesmo ritmo, então, uma máquina poda 100 m² por hora.
Assim, em 5 horas, uma máquina poda 500 m².
Queremos a poda de 8000 m² e precisamos determinar o número de máquinas necessárias. Basta dividir 8000 m² por 500 m²:
Então, são necessárias 16 máquinas para podar 8000 m² em 5 horas. No entanto, a questão não nos pergunta o número total de máquinas, mas sim o número mínimo de máquinas que o administrador do campo deverá solicitar ao clube vizinho.
Sabendo que o administrador já possui 2 máquinas, então, ele deve pedir apenas 16 – 2 = 14 máquinas emprestadas.
Alternativa correta: D
Você também pode se interessar:
- Exercícios de juros simples
- Exercícios sobre Teorema de Pitágoras
- Exercícios de divisão
- Divisão de números decimais – Veja como dividir números com vírgula
- Multiplicação de números decimais – Aprenda a multiplicar números com vírgula


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.